Номер №5, страница 21 - гдз по физике 7 класс самостоятельные и контрольные работы Шабусов

Авторы: Шабусов А. К.
Тип: Самостоятельные и контрольные работы
Издательство: Новое знание
Год издания: 2021 - 2026
Цвет обложки: салатовый
ISBN: 978-985-24-0249-1
Популярные ГДЗ в 7 классе
Лабораторные работы - номер №5, страница 21.
№№5 (с. 21)
Условие. №№5 (с. 21)
скриншот условия





Лабораторная работа № 5
Измерение плотности вещества (урок 31)
Вспоминаем изученное
Плотность обозначается греческой буквой ρ (ро).
Основной единицей плотности в СИ является 1 килограмм на метр кубический ($\frac{\text{кг}}{\text{м}^3}$). Используется и дольная единица измерения:
$1 \frac{\text{г}}{\text{см}^3} = 1000 \frac{\text{кг}}{\text{м}^3}$;
$1 \frac{\text{кг}}{\text{м}^3} = 0,001 \frac{\text{г}}{\text{см}^3}$.
Формула для нахождения плотности:
$\rho = \frac{m}{V}$
где $\text{ m}$ — масса тела; $\text{ V}$ — объем тела.
Измеряем массу тела на рычажных весах
Перед измерением массы необходимо уравновесить весы. Далеко не всегда чашки весов находятся на одном уровне. Во многих конструкциях есть специальные противовесы, которые можно регулировать. Если их нет, можно уравновесить чашки с помощью кусочков бумаги.
Когда чашки окажутся на одном уровне, на одну поставьте измеряемое тело (лучше на чашку с бумажками), а на другую поместите разновесы (гирьки). Вначале лучше ставить гирьку с большей массой. Если чашка с разновесами перевесит тело, замените ее гирькой меньшей массы. Продолжайте этот процесс до тех пор, пока чашки весов не уравновесятся. После этого суммируйте массу всех разновесов. Это и будет искомая масса тела.
Примечание. При измерении не имеет смысла брать разновесы массой менее 100 мг, так как данное значение близко к погрешности весов.
Измеряем плотность прямоугольного бруска
Измерьте длину $\text{ a}$, ширину $\text{ b}$ и высоту $\text{ c}$ бруска. Обратите внимание, что все размеры должны быть в сантиметрах. Сразу же занесите полученные данные в таблицу. Например:
| Наименование тела | Длина $\text{ a}$, см | Ширина $\text{ b}$, см | Высота $\text{ c}$, см | Объем $\text{ V}$, см³ | Масса $\text{ m}$, г | Плотность | |
|---|---|---|---|---|---|---|---|
| $\rho, \frac{г}{см^3}$ | $\rho, \frac{\text{кг}}{\text{м}^3}$ | ||||||
| Брусок | 9,6 | 4,5 | 3,1 | ||||
Объем бруска вычислите по формуле
$V = abc$.
Измерьте на весах массу бруска и рассчитайте его плотность по формуле
$\rho = \frac{m}{V}$.
Совершенно секретно. Как правильно округлять результат измерений
При расчетах часто получается, что калькулятор выдает не «красивый» целый результат, а «длинное» число. В этом случае ответ нужно округлить. Разберемся, как правильно это сделать на примере определения плотности бруска.
При измерении объема бруска мы перемножили его длину $\text{a}$, ширину $\text{b}$ и высоту $\text{c}$:
$V = 9,6 \text{ см} \cdot 4,5 \text{ см} \cdot 3,1 \text{ см} = 133,92 \text{ см}^3$.
Несмотря на то что все множители даны с точностью до десятых, ответ не будет иметь такую высокую точность. При перемножении не нужно обращать внимание на разряды цифр. Гораздо важнее, сколько цифр в каждом множителе, не считая начальных и конечных нулей. Столько же цифр должно быть в ответе. При этом ориентироваться нужно на множитель с наименьшим количеством цифр. Аналогично нужно действовать при делении величин.
В приведенном примере все множители имеют по две цифры, поэтому и ответ должен содержать две цифры, не считая начальных и конечных нулей:
$V = 133,92 \text{ см}^3 = 130 \text{ см}^3$.
Однако это промежуточное значение, поэтому для получения более точного результата его лучше не округлять. Дело в том, что каждое действие приводит к дополнительной погрешности, поэтому чем больше цифр в промежуточных данных, тем точнее результат.
Вернемся к расчету плотности. Допустим, масса бруска $m = 381,2$ г. Тогда
$\rho = \frac{381,2 \text{ г}}{133,92 \text{ см}^3} = 2,8464755 \frac{\text{г}}{\text{см}^3}$.
Это конечный результат. Как мы выяснили, объем получен с точностью до двух цифр. И несмотря на то что масса измерена с точностью до четырех цифр, полученный результат достаточно округлить до двух, то есть
$\rho = 2,8464755 \frac{\text{г}}{\text{см}^3} = 2,8 \frac{\text{г}}{\text{см}^3} = 2800 \frac{\text{кг}}{\text{м}^3}$.
Чтобы показать, сколько цифр должен содержать ответ, в условии задачи указывают значения до нужного количества цифр, даже если это нули. Например:
$s = 3,00 \text{ м}$;
$\Delta t = 0,120 \text{ мин}$.
В обоих случаях значения величин указаны с тремя значащими цифрами.
При сложении величин учитывается не количество значащих цифр, а их разряды. Например:
$2,37322222 \text{ м} + 0,4 \text{ м} = 2,8 \text{ м}$;
$235 \text{ кг} + 0,08 \text{ кг} = 235 \text{ кг}$.
Примечание. Напомним, что при округлении начальные и конечные нули не учитываются. Ниже приведены правильные округления величин до двух цифр.
$2,37322222 \text{ м} \approx 2,4 \text{ м}$;
$0,237322222 \text{ м} \approx 0,24 \text{ м}$;
$0,000237322222 \text{ м} \approx 0,00024 \text{ м}$;
$237,322222 \text{ м} \approx 240 \text{ м}$;
$2373,22222 \text{ м} \approx 2400 \text{ м}$;
$2373222,222 \text{ м} \approx 2400000 \text{ м}$.
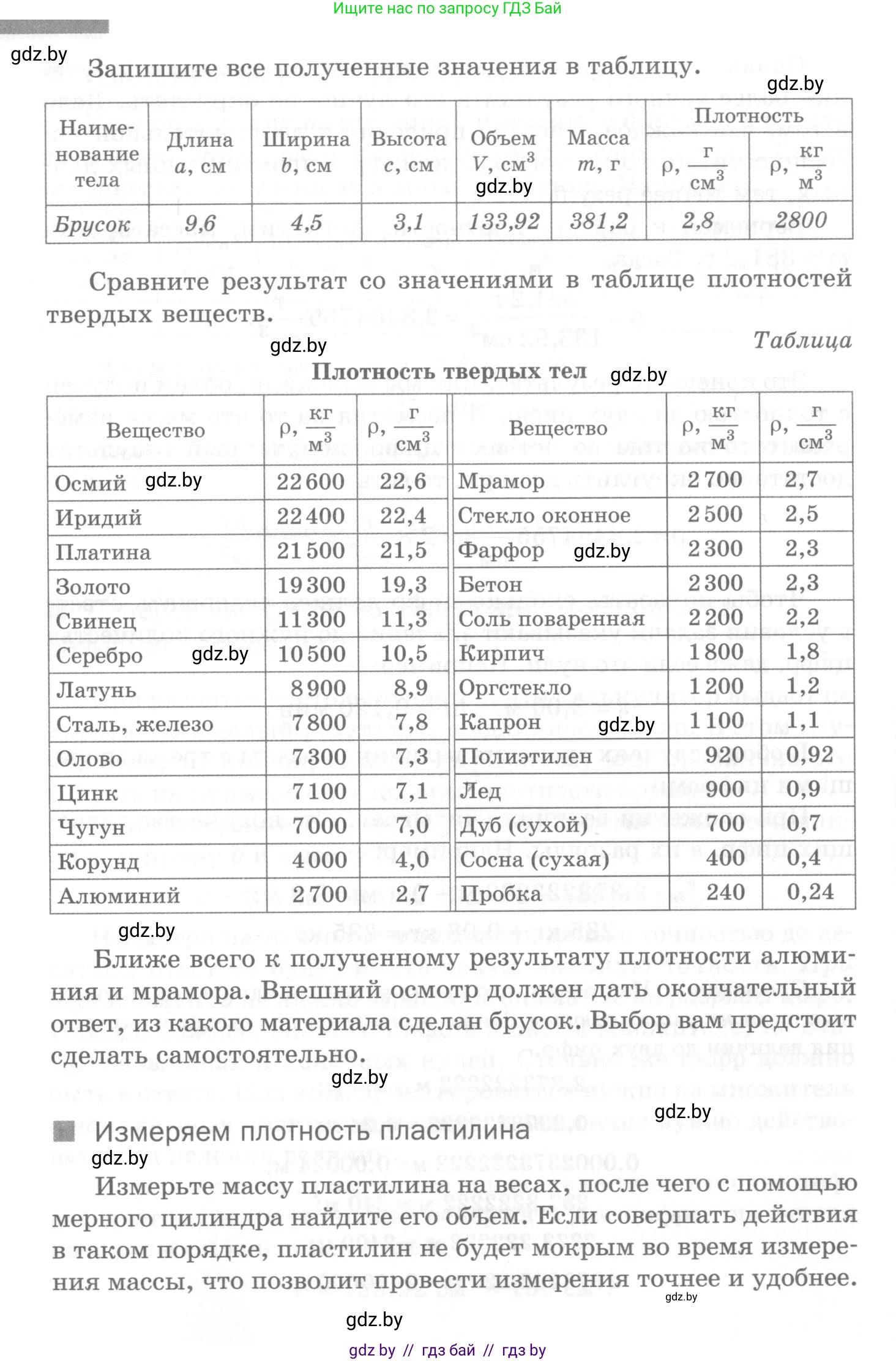
Запишите все полученные значения в таблицу.
| Наименование тела | Длина $\text{ a}$, см | Ширина $\text{ b}$, см | Высота $\text{ c}$, см | Объем $\text{ V}$, см³ | Масса $\text{ m}$, г | Плотность | |
|---|---|---|---|---|---|---|---|
| $\rho, \frac{\text{г}}{\text{см}^3}$ | $\rho, \frac{\text{кг}}{\text{м}^3}$ | ||||||
| Брусок | 9,6 | 4,5 | 3,1 | 133,92 | 381,2 | 2,8 | 2800 |
Сравните результат со значениями в таблице плотностей твердых веществ.
Таблица Плотность твердых тел
| Вещество | $\rho, \frac{\text{кг}}{\text{м}^3}$ | $\rho, \frac{\text{г}}{\text{см}^3}$ | Вещество | $\rho, \frac{\text{кг}}{\text{м}^3}$ | $\rho, \frac{\text{г}}{\text{см}^3}$ |
|---|---|---|---|---|---|
| Осмий | 22600 | 22,6 | Мрамор | 2700 | 2,7 |
| Иридий | 22400 | 22,4 | Стекло оконное | 2500 | 2,5 |
| Платина | 21500 | 21,5 | Фарфор | 2300 | 2,3 |
| Золото | 19300 | 19,3 | Бетон | 2300 | 2,3 |
| Свинец | 11300 | 11,3 | Соль поваренная | 2200 | 2,2 |
| Серебро | 10500 | 10,5 | Кирпич | 1800 | 1,8 |
| Латунь | 8900 | 8,9 | Оргстекло | 1200 | 1,2 |
| Сталь, железо | 7800 | 7,8 | Капрон | 1100 | 1,1 |
| Олово | 7300 | 7,3 | Полиэтилен | 920 | 0,92 |
| Цинк | 7100 | 7,1 | Лед | 900 | 0,9 |
| Чугун | 7000 | 7,0 | Дуб (сухой) | 700 | 0,7 |
| Корунд | 4000 | 4,0 | Сосна (сухая) | 400 | 0,4 |
| Алюминий | 2700 | 2,7 | Пробка | 240 | 0,24 |
Ближе всего к полученному результату плотности алюминия и мрамора. Внешний осмотр должен дать окончательный ответ, из какого материала сделан брусок. Выбор вам предстоит сделать самостоятельно.
Измеряем плотность пластилина
Измерьте массу пластилина на весах, после чего с помощью мерного цилиндра найдите его объем. Если совершать действия в таком порядке, пластилин не будет мокрым во время измерения массы, что позволит провести измерения точнее и удобнее.
Обратите внимание, что пластилин тонет в воде, поэтому его плотность будет больше $1 \frac{\text{г}}{\text{см}^3}$. плотность пластилина примерно равна $1,2 \frac{\text{г}}{\text{см}^3}$. Поэтому если полученный результат сильно отличается от этого значения, проведите измерения повторно.
Полученные данные внесите в таблицу. Например:
| Наименование тела | Длина $\text{ a}$, см | Ширина $\text{ b}$, см | Высота $\text{ c}$, см | Объем $\text{ V}$, см³ | Масса $\text{ m}$, г | Плотность | |
|---|---|---|---|---|---|---|---|
| $\rho, \frac{\text{г}}{\text{см}^3}$ | $\rho, \frac{\text{кг}}{\text{м}^3}$ | ||||||
| Брусок | 9,6 | 4,5 | 3,1 | 133,92 | 381,2 | 2,85 | 2850 |
| Кусок пластилина | — | — | — | 55 | 70,6 | 1,3 | 1300 |
Вспоминаем про точность измерения
Любое измерение всегда имеет некоторую погрешность, которая возникает из-за ряда причин. Это погрешность прибора, человеческий фактор, сложности измерения, влияние внешних условий и др. Например, при измерении массы тела на весах погрешность может составить несколько грамм.
Если тело небольшое, то может возникнуть ситуация, когда погрешность измерения больше, чем масса тела. В этом случае используют способ измерения малых величин, о котором мы говорили ранее.
Напомним, при измерении малых величин измеряют не одно тело, а сразу несколько. Например, при измерении массы кнопки правильнее измерить массу 20 кнопок, а потом полученный результат разделить на 20. В этом случае погрешность также уменьшится в 20 раз.
Пишем выводы
В выводах к данной работе нужно указать, что вы измеряли, каким способом.
Например:
«В ходе выполнения работы мы измерили плотность бруска, предварительно измерив и рассчитав его объем и массу, а плотность вычислили по формуле. Определили материал, из которого состоит брусок: _________. Расхождение между табличным значением и полученным результатом объясняется погрешностью измерений.
Измерили плотность куска пластилина, определив его объем прямыми измерениями с помощью мерного цилиндра, а плотность вычислили по формуле».
Решение. №№5 (с. 21)
Запишите все полученные значения в таблицу.
Для определения плотности прямоугольного бруска, необходимо сначала вычислить его объем, а затем, зная массу, найти плотность.
Дано:
Длина бруска, $a = 9,6$ см
Ширина бруска, $b = 4,5$ см
Высота бруска, $c = 3,1$ см
Масса бруска, $m = 381,2$ г
$a = 9,6 \text{ см} = 0,096 \text{ м}$
$b = 4,5 \text{ см} = 0,045 \text{ м}$
$c = 3,1 \text{ см} = 0,031 \text{ м}$
$m = 381,2 \text{ г} = 0,3812 \text{ кг}$
Найти:
Объем бруска $\text{V}$ в см3, плотность бруска $\rho$ в $\frac{\text{г}}{\text{см}^3}$ и $\frac{\text{кг}}{\text{м}^3}$.
Решение:
1. Вычислим объем бруска по формуле $V = abc$.
$V = 9,6 \text{ см} \cdot 4,5 \text{ см} \cdot 3,1 \text{ см} = 133,92 \text{ см}^3$.
2. Рассчитаем плотность бруска по формуле $\rho = \frac{m}{V}$.
$\rho = \frac{381,2 \text{ г}}{133,92 \text{ см}^3} \approx 2,8464755... \frac{\text{г}}{\text{см}^3}$.
Согласно правилам округления, результат должен содержать столько значащих цифр, сколько их в множителе с наименьшим количеством значащих цифр. В измерениях длины, ширины и высоты (9,6; 4,5; 3,1) по две значащих цифры. Следовательно, итоговый результат для плотности нужно округлить до двух значащих цифр.
$\rho \approx 2,8 \frac{\text{г}}{\text{см}^3}$.
3. Переведем плотность в единицы СИ ($\frac{\text{кг}}{\text{м}^3}$), зная, что $1 \frac{\text{г}}{\text{см}^3} = 1000 \frac{\text{кг}}{\text{м}^3}$.
$\rho = 2,8 \frac{\text{г}}{\text{см}^3} \cdot 1000 = 2800 \frac{\text{кг}}{\text{м}^3}$.
Заполним таблицу на основе полученных данных.
| Наименование тела | Длина a, см | Ширина b, см | Высота c, см | Объем V, см3 | Масса m, г | Плотность | |
|---|---|---|---|---|---|---|---|
| $\rho, \frac{\text{г}}{\text{см}^3}$ | $\rho, \frac{\text{кг}}{\text{м}^3}$ | ||||||
| Брусок | 9,6 | 4,5 | 3,1 | 133,92 | 381,2 | 2,8 | 2800 |
Ответ: Объем бруска равен 133,92 см3, его плотность составляет 2,8 г/см3 или 2800 кг/м3. Заполненная таблица представлена выше.
Сравните результат со значениями в таблице плотностей твердых веществ.
Решение:
Полученное значение плотности бруска $\rho = 2800 \frac{\text{кг}}{\text{м}^3}$. Сравним это значение с табличными данными. Наиболее близкие значения плотности у алюминия ($\rho = 2700 \frac{\text{кг}}{\text{м}^3}$) и мрамора ($\rho = 2700 \frac{\text{кг}}{\text{м}^3}$). Расхождение между вычисленным и табличным значением может быть объяснено погрешностями измерений линейных размеров и массы бруска. Для окончательного определения материала необходим визуальный осмотр.
Ответ: Плотность бруска (2800 кг/м3) наиболее близка к плотности алюминия или мрамора (2700 кг/м3). Вероятно, брусок сделан из одного из этих материалов.
Измеряем плотность пластилина
Рассчитаем плотность пластилина, используя данные из примера.
Дано:
Объем куска пластилина, $V = 55 \text{ см}^3$
Масса куска пластилина, $m = 70,6 \text{ г}$
$V = 55 \text{ см}^3 = 0,000055 \text{ м}^3$
$m = 70,6 \text{ г} = 0,0706 \text{ кг}$
Найти:
Плотность пластилина $\rho$ в $\frac{\text{г}}{\text{см}^3}$ и $\frac{\text{кг}}{\text{м}^3}$.
Решение:
1. Рассчитаем плотность пластилина по формуле $\rho = \frac{m}{V}$.
$\rho = \frac{70,6 \text{ г}}{55 \text{ см}^3} \approx 1,2836... \frac{\text{г}}{\text{см}^3}$.
Применяя правила округления, учитываем, что объем (55 см3) измерен с точностью до двух значащих цифр, а масса (70,6 г) — до трех. Результат следует округлить до наименьшего числа значащих цифр, то есть до двух.
$\rho \approx 1,3 \frac{\text{г}}{\text{см}^3}$.
2. Переведем плотность в единицы СИ.
$\rho = 1,3 \frac{\text{г}}{\text{см}^3} \cdot 1000 = 1300 \frac{\text{кг}}{\text{м}^3}$.
Ответ: Плотность куска пластилина составляет 1,3 г/см3 или 1300 кг/м3.
Пишем выводы
Решение:
Заполним шаблон для выводов на основе проведенных расчетов.
Ответ:
В ходе выполнения работы мы измерили плотность бруска, предварительно измерив его размеры (длину, ширину, высоту), рассчитав объем и измерив массу. Плотность мы вычислили по формуле $\rho = \frac{m}{V}$. Определили материал, из которого состоит брусок: алюминий или мрамор. Расхождение между табличным значением (2700 кг/м3) и полученным результатом (2800 кг/м3) объясняется погрешностью измерений.
Измерили плотность куска пластилина, определив его объем прямыми измерениями с помощью мерного цилиндра (согласно условиям примера), а плотность вычислили по формуле. Полученное значение плотности (1300 кг/м3) близко к ожидаемому для пластилина.
Другие задания:
Помогло решение? Оставьте отзыв в комментариях ниже.
Присоединяйтесь к Телеграм-группе @gdz_by_belarus
ПрисоединитьсяМы подготовили для вас ответ c подробным объяснением домашего задания по физике за 7 класс, для упражнения номер №5 расположенного на странице 21 к самостоятельным и контрольным работам 2021 года издания для учащихся школ и гимназий.
Теперь на нашем сайте ГДЗ.ТОП вы всегда легко и бесплатно найдёте условие с правильным ответом на вопрос «Как решить ДЗ» и «Как сделать» задание по физике к упражнению №№5 (с. 21), автора: Шабусов (Анатолий Константинович), учебного пособия издательства Новое знание.













