Номер 2, страница 17 - гдз по физике 7 класс обучающая тетрадь Шабусов, Дубина

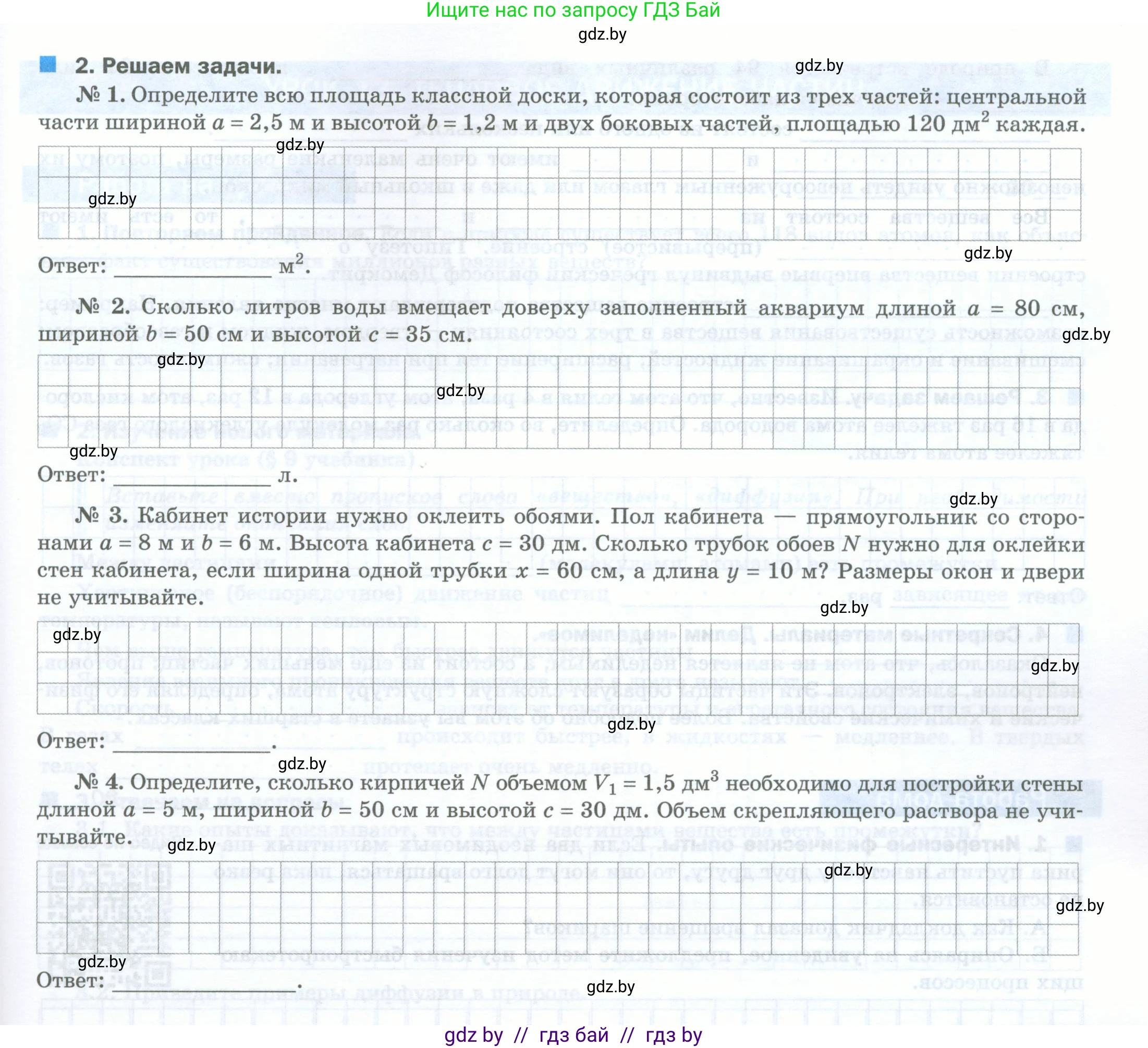
2. Решаем задачи.

№ 1. Определите всю площадь классной доски, которая состоит из трех частей: центральной части шириной $a = 2,5\text{ м}$ и высотой $b = 1,2\text{ м}$ и двух боковых частей, площадью $120\text{ дм}^2$ каждая.

Ответ: _____ $\text{м}^2$.

№ 2. Сколько литров воды вмещает доверху заполненный аквариум длиной $a = 80\text{ см}$, шириной $b = 50\text{ см}$ и высотой $c = 35\text{ см}$.

Ответ: _____ л.

№ 3. Кабинет истории нужно оклеить обоями. Пол кабинета — прямоугольник со сторонами $a = 8\text{ м}$ и $b = 6\text{ м}$. Высота кабинета $c = 30\text{ дм}$. Сколько трубок обоев $\text{N}$ нужно для оклейки стен кабинета, если ширина одной трубки $x = 60\text{ см}$, а длина $y = 10\text{ м}$? Размеры окон и двери не учитывайте.

Ответ: _____ .

№ 4. Определите, сколько кирпичей $\text{N}$ объемом $V_1 = 1,5\text{ дм}^3$ необходимо для постройки стены длиной $a = 5\text{ м}$, шириной $b = 50\text{ см}$ и высотой $c = 30\text{ дм}$. Объем скрепляющего раствора не учитывайте.

Ответ: _____ .

№ 1.

Чтобы найти общую площадь классной доски, нужно сложить площади всех ее трех частей: центральной и двух боковых.

1. Найдем площадь центральной части. Она имеет форму прямоугольника, поэтому ее площадь $S_1$ равна произведению ширины $\text{a}$ на высоту $\text{b}$.

$a = 2,5$ м

$b = 1,2$ м

$S_1 = a \times b = 2,5 \text{ м} \times 1,2 \text{ м} = 3 \text{ м}^2$

2. Площадь каждой из двух боковых частей дана в квадратных дециметрах ($S_2 = 120 \text{ дм}^2$). Переведем эту площадь в квадратные метры, зная, что $1 \text{ м}^2 = 100 \text{ дм}^2$.

$S_2 = 120 \text{ дм}^2 = \frac{120}{100} \text{ м}^2 = 1,2 \text{ м}^2$

3. Так как боковых частей две, их общая площадь составляет:

$2 \times S_2 = 2 \times 1,2 \text{ м}^2 = 2,4 \text{ м}^2$

4. Теперь сложим площадь центральной части и общую площадь боковых частей, чтобы найти общую площадь доски $S_{общ}$.

$S_{общ} = S_1 + 2 \times S_2 = 3 \text{ м}^2 + 2,4 \text{ м}^2 = 5,4 \text{ м}^2$

Ответ: 5,4 м².

№ 2.

Дано:

Длина аквариума, $a = 80$ см

Ширина аквариума, $b = 50$ см

Высота аквариума, $c = 35$ см

$a = 80 \text{ см} = 0,8 \text{ м}$
$b = 50 \text{ см} = 0,5 \text{ м}$
$c = 35 \text{ см} = 0,35 \text{ м}$

Найти:

Объем воды $\text{V}$ в литрах.

Решение:

1. Объем аквариума, имеющего форму прямоугольного параллелепипеда, вычисляется по формуле:

$V = a \times b \times c$

Подставим значения в системе СИ (метры):

$V = 0,8 \text{ м} \times 0,5 \text{ м} \times 0,35 \text{ м} = 0,14 \text{ м}^3$

2. Чтобы перевести объем из кубических метров в литры, воспользуемся соотношением: $1 \text{ м}^3 = 1000$ литров.

$V = 0,14 \times 1000 \text{ л} = 140 \text{ л}$

Ответ: 140 л.

№ 3.

Дано:

Длина кабинета, $a = 8$ м

Ширина кабинета, $b = 6$ м

Высота кабинета, $c = 30$ дм

Ширина трубки обоев, $x = 60$ см

Длина трубки обоев, $y = 10$ м

$c = 30 \text{ дм} = 3 \text{ м}$
$x = 60 \text{ см} = 0,6 \text{ м}$

Найти:

Количество трубок обоев $\text{N}$.

Решение:

1. Найдем площадь стен, которые нужно оклеить. Это боковая поверхность прямоугольного параллелепипеда. Она равна произведению периметра основания на высоту.

Периметр пола: $P = 2 \times (a + b) = 2 \times (8 \text{ м} + 6 \text{ м}) = 2 \times 14 \text{ м} = 28 \text{ м}$

Площадь стен: $S_{стен} = P \times c = 28 \text{ м} \times 3 \text{ м} = 84 \text{ м}^2$

2. Найдем площадь одной трубки (рулона) обоев.

$S_{трубки} = x \times y = 0,6 \text{ м} \times 10 \text{ м} = 6 \text{ м}^2$

3. Разделим площадь стен на площадь одной трубки, чтобы найти необходимое количество трубок.

$N = \frac{S_{стен}}{S_{трубки}} = \frac{84 \text{ м}^2}{6 \text{ м}^2} = 14$

Ответ: 14 трубок.

№ 4.

Дано:

Объем одного кирпича, $V_1 = 1,5$ дм³

Длина стены, $a = 5$ м

Ширина стены, $b = 50$ см

Высота стены, $c = 30$ дм

$V_1 = 1,5 \text{ дм}^3 = 0,0015 \text{ м}^3$
$b = 50 \text{ см} = 0,5 \text{ м}$
$c = 30 \text{ дм} = 3 \text{ м}$

Найти:

Количество кирпичей $\text{N}$.

Решение:

1. Найдем общий объем стены $V_{стены}$, которая имеет форму прямоугольного параллелепипеда.

$V_{стены} = a \times b \times c$

Подставим значения в системе СИ (метры):

$V_{стены} = 5 \text{ м} \times 0,5 \text{ м} \times 3 \text{ м} = 7,5 \text{ м}^3$

2. Чтобы найти количество кирпичей, необходимых для постройки, разделим объем стены на объем одного кирпича.

$N = \frac{V_{стены}}{V_1} = \frac{7,5 \text{ м}^3}{0,0015 \text{ м}^3} = 5000$

Ответ: 5000 кирпичей.