Номер 2, страница 24 - гдз по физике 7 класс обучающая тетрадь Шабусов, Дубина

2. Решаем задачи. «Физкультминутка».

№ 1. Один спортсмен пробежал 8 кругов за $\Delta t_1 = 20$ мин, а второй — 10 кругов за $\Delta t_2 = 0,375$ ч. Кто из них пробегал 1 круг быстрее и на сколько?

Ответ: _____ с.

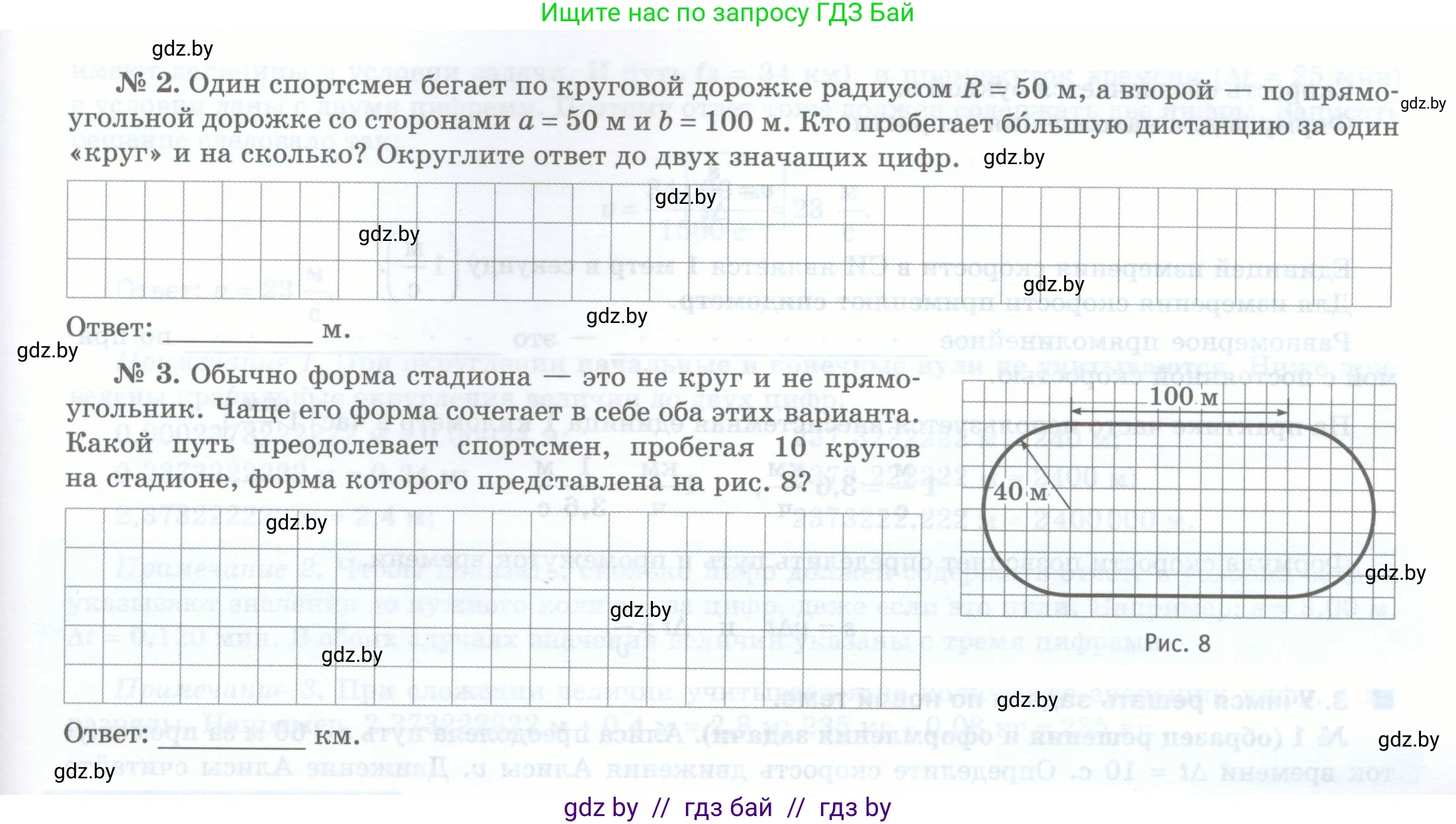
№ 2. Один спортсмен бегает по круговой дорожке радиусом $R = 50$ м, а второй — по прямоугольной дорожке со сторонами $a = 50$ м и $b = 100$ м. Кто пробегает большую дистанцию за один «круг» и на сколько? Округлите ответ до двух значащих цифр.

Ответ: _____ м.

№ 3. Обычно форма стадиона — это не круг и не прямоугольник. Чаще его форма сочетает в себе оба этих варианта. Какой путь преодолевает спортсмен, пробегая 10 кругов на стадионе, форма которого представлена на рис. 8?

Рис. 8

Ответ: _____ км.

№ 1.

Дано:

Первый спортсмен: $n_1 = 8$ кругов, $\Delta t_1 = 20$ мин.
Второй спортсмен: $n_2 = 10$ кругов, $\Delta t_2 = 0,375$ ч.
Перевод в СИ:
$\Delta t_1 = 20 \text{ мин} = 20 \cdot 60 \text{ с} = 1200 \text{ с}$
$\Delta t_2 = 0,375 \text{ ч} = 0,375 \cdot 3600 \text{ с} = 1350 \text{ с}$

Найти:

Кто пробежал 1 круг быстрее и на сколько?

Решение:

Чтобы определить, кто пробежал круг быстрее, нужно найти время, затраченное каждым спортсменом на один круг.
1. Время одного круга для первого спортсмена ($t_1$):
$t_1 = \frac{\Delta t_1}{n_1} = \frac{1200 \text{ с}}{8} = 150 \text{ с}$
2. Время одного круга для второго спортсмена ($t_2$):
$t_2 = \frac{\Delta t_2}{n_2} = \frac{1350 \text{ с}}{10} = 135 \text{ с}$
3. Сравним время: $135 \text{ с} < 150 \text{ с}$, следовательно, второй спортсмен пробегает один круг быстрее.
4. Найдем разницу во времени ($\Delta t$):
$\Delta t = t_1 - t_2 = 150 \text{ с} - 135 \text{ с} = 15 \text{ с}$

Ответ: второй спортсмен пробегал 1 круг быстрее на 15 с.

№ 2.

Дано:

Первый спортсмен (круговая дорожка): радиус $R = 50$ м.
Второй спортсмен (прямоугольная дорожка): стороны $a = 50$ м, $b = 100$ м.

Найти:

Кто пробегает большую дистанцию за один «круг» и на сколько ($\Delta L$)? Округлить до двух значащих цифр.

Решение:

1. Найдем дистанцию одного круга для первого спортсмена ($L_1$). Это длина окружности:
$L_1 = 2 \pi R = 2 \cdot \pi \cdot 50 \text{ м} = 100 \pi \text{ м} \approx 100 \cdot 3,1416 \text{ м} \approx 314,16 \text{ м}$
2. Найдем дистанцию одного «круга» для второго спортсмена ($L_2$). Это периметр прямоугольника:
$L_2 = 2(a + b) = 2(50 \text{ м} + 100 \text{ м}) = 2 \cdot 150 \text{ м} = 300 \text{ м}$
3. Сравним дистанции: $314,16 \text{ м} > 300 \text{ м}$, следовательно, первый спортсмен пробегает большую дистанцию.
4. Найдем разницу в дистанциях ($\Delta L$):
$\Delta L = L_1 - L_2 \approx 314,16 \text{ м} - 300 \text{ м} = 14,16 \text{ м}$
5. Округлим результат до двух значащих цифр:
$\Delta L \approx 14 \text{ м}$

Ответ: первый спортсмен пробегает большую дистанцию на 14 м.

№ 3.

Дано:

Форма стадиона: два прямых участка и два полукруга.
Длина прямого участка: $l = 100$ м.
Радиус полукруга: $r = 40$ м (согласно рис. 8).
Количество кругов: $n = 10$.

Найти:

Общий путь, который преодолевает спортсмен ($\text{S}$), в км.

Решение:

1. Найдем длину одного круга на стадионе ($L_{круг}$). Она складывается из длины двух прямых участков и длины двух полукругов, которые вместе составляют одну окружность.
Длина двух прямых участков: $L_{прям.} = 2 \cdot l = 2 \cdot 100 \text{ м} = 200 \text{ м}$
Длина двух полукругов (одной окружности): $L_{окр.} = 2 \pi r = 2 \cdot \pi \cdot 40 \text{ м} = 80 \pi \text{ м}$
Общая длина одного круга: $L_{круг} = L_{прям.} + L_{окр.} = (200 + 80 \pi) \text{ м}$
Используя приближенное значение $\pi \approx 3,14$, получим:
$L_{круг} \approx 200 \text{ м} + 80 \cdot 3,14 \text{ м} = 200 \text{ м} + 251,2 \text{ м} = 451,2 \text{ м}$
2. Найдем общий путь ($\text{S}$), который преодолевает спортсмен за 10 кругов:
$S = n \cdot L_{круг} = 10 \cdot 451,2 \text{ м} = 4512 \text{ м}$
3. Переведем результат в километры, зная, что $1 \text{ км} = 1000 \text{ м}$:
$S = \frac{4512}{1000} \text{ км} = 4,512 \text{ км}$

Ответ: 4,512 км.