Номер 2, страница 64 - гдз по физике 7 класс обучающая тетрадь Шабусов, Дубина

Авторы: Шабусов А. К., Дубина М. В., Батурчик Б. П.
Тип: обучающая тетрадь
Издательство: Новое знание
Год издания: 2021 - 2026
Цвет обложки: жёлтый
ISBN: 978-985-24-0247-7
Популярные ГДЗ в 7 классе
Урок 40. Решение задач по теме «Сложение сил. Равнодействующая сил». Работа на уроке - номер 2, страница 64.
№2 (с. 64)
Условие. №2 (с. 64)
скриншот условия
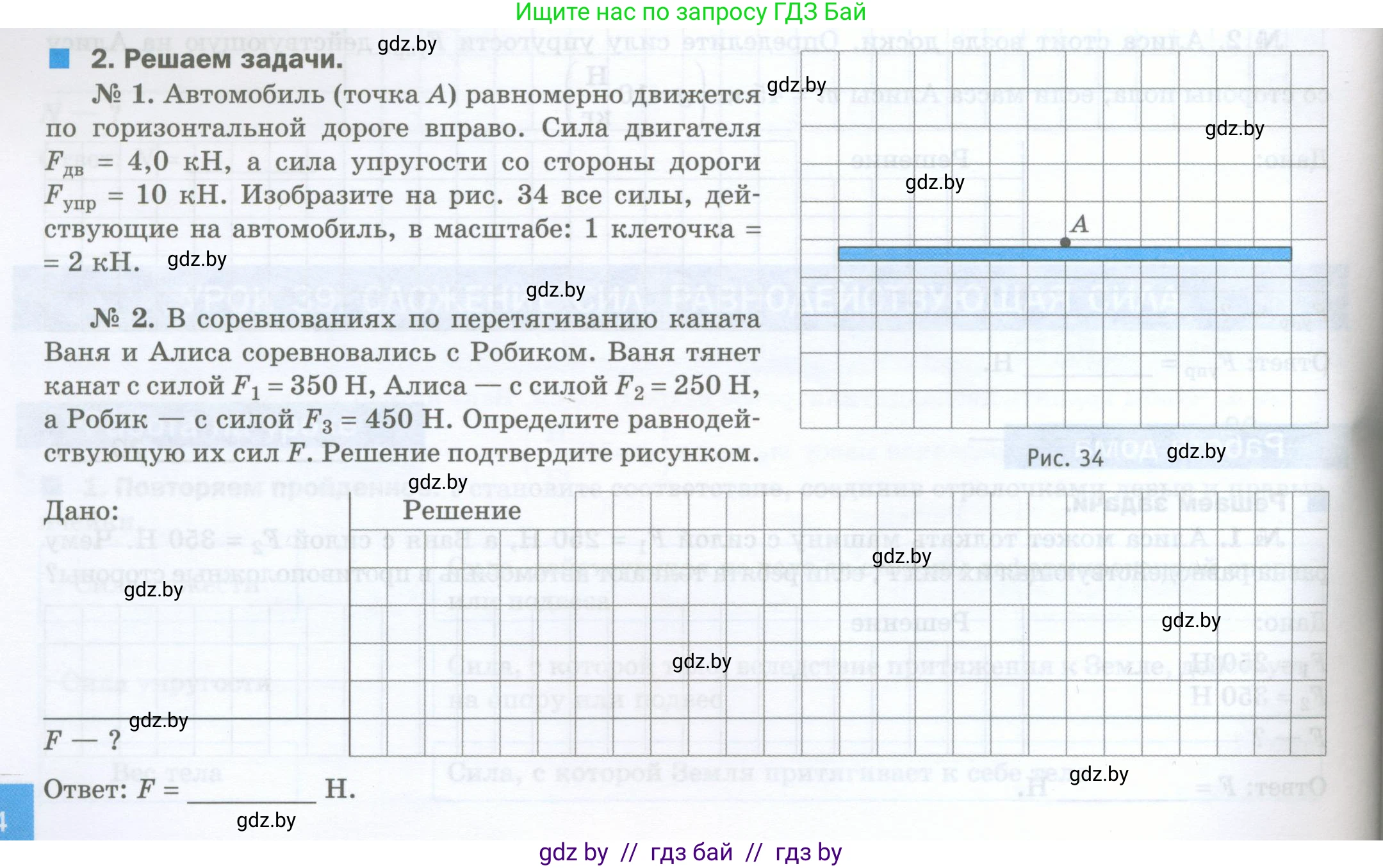
2. Решаем задачи.
№ 1. Автомобиль (точка А) равномерно движется по горизонтальной дороге вправо. Сила двигателя $F_{\text{дв}} = 4,0 \text{ кН}$, а сила упругости со стороны дороги $F_{\text{упр}} = 10 \text{ кН}$. Изобразите на рис. 34 все силы, действующие на автомобиль, в масштабе: $1 \text{ клеточка} = 2 \text{ кН}$.
Рис. 34
№ 2. В соревнованиях по перетягиванию каната Ваня и Алиса соревновались с Робиком. Ваня тянет канат с силой $F_1 = 350 \text{ Н}$, Алиса — с силой $F_2 = 250 \text{ Н}$, а Робик — с силой $F_3 = 450 \text{ Н}$. Определите равнодействующую их сил $\text{F}$. Решение подтвердите рисунком.
| Дано: | Решение |
| $F - ?$ |
Ответ: $F = \_\_\_\_\_\_\_$ Н.
№ 3. Ваня и Алиса несут носилки с сухими листьями массой $m = 15 \text{ кг}$. Ваня прикладывает силу $F_1 = 80 \text{ Н}$. Определите, какую силу $F_2$ прикладывает Алиса ($g = 10 \frac{\text{Н}}{\text{кг}}$).
| Дано: | Решение |
| $F_2 - ?$ |
Ответ: $F_2 = \_\_\_\_\_\_\_$ Н.
№ 4. Посадил Дедка репку. Выросла она большая-пребольшая, поэтому Дедка тянул Репку с силой $F_1 = 250 \text{ Н}$, Бабка тянула Дедку с силой $F_2 = 150 \text{ Н}$, Внучка тянула Бабку с силой $F_3 = 100 \text{ Н}$, Жучка за Внучку с силой $F_4 = 35 \text{ Н}$, Кошка за Жучку с силой $F_5 = 14 \text{ Н}$. Определите силу $F_6$, которую нужно приложить Мышке, чтобы вытащить Репку, если та держится за землю с силой $F = 550 \text{ Н}$.
| Дано: | Решение |
| $F_6 - ?$ |
Ответ: $F_6 = \_\_\_\_\_\_\_$ Н.
№ 5. Оловянный ($\rho = 7,3 \frac{\text{г}}{\text{см}^3}$) кубик со стороной $a = 3,0 \text{ см}$ лежит на столе. Определите силу упругости $F_{\text{упр}}$, которая действует на кубик со стороны стола ($g = 10 \frac{\text{Н}}{\text{кг}}$).
| Дано: | Решение |
| $F_{\text{упр}} - ?$ |
Ответ: $F_{\text{упр}} = \_\_\_\_\_\_\_$ Н.
№ 6. Гоночный автомобиль массой $m = 1,5 \text{ т}$ равномерно движется по горизонтальной трассе. Сила двигателя $F_{\text{дв}}$, которая толкает автомобиль вперед, в 3 раза меньше силы упругости $F_{\text{упр}}$, действующей на автомобиль со стороны дороги. Определите силу сопротивления движению $F_{\text{сопр}}$ ($g = 10 \frac{\text{Н}}{\text{кг}}$). Решение подтвердите рисунком.
| Дано: | Решение |
| $F_{\text{сопр}} - ?$ |
Ответ: $F_{\text{сопр}} = \_\_\_\_\_\_\_$ кН.
Ршение. №2 (с. 64)
№ 1.
Дано:
$F_{дв} = 4,0 \text{ кН}$
$F_{упр} = 10 \text{ кН}$
Масштаб: 1 клеточка = 2 кН
Автомобиль движется равномерно.
Решение:
На автомобиль действуют четыре силы:
1. Сила тяги двигателя $F_{дв}$, направленная вправо (по ходу движения). Её модуль равен $4,0 \text{ кН}$. В заданном масштабе это вектор длиной $4,0 \text{ кН} / 2 \text{ кН/кл} = 2$ клеточки.
2. Сила сопротивления движению $F_{сопр}$, направленная влево (против движения). Так как автомобиль движется равномерно, то по первому закону Ньютона равнодействующая всех сил равна нулю. Это означает, что горизонтальные силы скомпенсированы. Следовательно, $F_{сопр} = F_{дв} = 4,0 \text{ кН}$. В заданном масштабе это вектор длиной $4,0 \text{ кН} / 2 \text{ кН/кл} = 2$ клеточки.
3. Сила упругости (реакции опоры) $F_{упр}$, действующая со стороны дороги, направлена вертикально вверх. Её модуль равен $10 \text{ кН}$. В заданном масштабе это вектор длиной $10 \text{ кН} / 2 \text{ кН/кл} = 5$ клеточек.
4. Сила тяжести $F_{тяж}$, действующая на автомобиль, направлена вертикально вниз. Так как автомобиль не движется по вертикали, вертикальные силы также скомпенсированы. Следовательно, $F_{тяж} = F_{упр} = 10 \text{ кН}$. В заданном масштабе это вектор длиной $10 \text{ кН} / 2 \text{ кН/кл} = 5$ клеточек.
Все силы приложены к центру автомобиля (точке А). Для изображения на рисунке необходимо от точки А отложить:
- вектор длиной 2 клетки вправо ($F_{дв}$)
- вектор длиной 2 клетки влево ($F_{сопр}$)
- вектор длиной 5 клеток вверх ($F_{упр}$)
- вектор длиной 5 клеток вниз ($F_{тяж}$)
Ответ: Силы изображены на рисунке согласно описанию: сила тяги (2 клетки вправо), сила сопротивления (2 клетки влево), сила упругости (5 клеток вверх) и сила тяжести (5 клеток вниз).
№ 2.
Дано:
$F_1 = 350 \text{ Н}$
$F_2 = 250 \text{ Н}$
$F_3 = 450 \text{ Н}$
Найти:
$F - ?$
Решение:
Ваня и Алиса тянут канат в одну сторону. Их суммарная сила $F_{12}$ направлена в одну сторону и равна сумме их сил:
$F_{12} = F_1 + F_2 = 350 \text{ Н} + 250 \text{ Н} = 600 \text{ Н}$.
Робик тянет канат в противоположную сторону с силой $F_3 = 450 \text{ Н}$.
Равнодействующая сила $\text{F}$ равна разности сил, действующих в противоположных направлениях. Она будет направлена в сторону большей силы.
$F = F_{12} - F_3 = 600 \text{ Н} - 450 \text{ Н} = 150 \text{ Н}$.
Равнодействующая сила направлена в сторону Вани и Алисы.
Подтверждение рисунком: Выберем масштаб, например, 1 клетка = 50 Н. Тогда от одной точки нужно отложить:
- Векторы сил $F_1$ (длиной $350/50 = 7$ клеток) и $F_2$ (длиной $250/50 = 5$ клеток) в одну сторону (например, влево). Их сумма — вектор длиной 12 клеток влево.
- Вектор силы $F_3$ (длиной $450/50 = 9$ клеток) в противоположную сторону (вправо).
- Равнодействующая будет вектором, равным разности длин векторов, направленным в сторону большего вектора, то есть влево. Длина этого вектора будет $12 - 9 = 3$ клетки. В нашем масштабе это соответствует силе $3 \cdot 50 \text{ Н} = 150 \text{ Н}$.
Ответ: $F = 150 \text{ Н}$.
№ 3.
Дано:
$m = 15 \text{ кг}$
$F_1 = 80 \text{ Н}$
$g = 10 \frac{\text{Н}}{\text{кг}}$
Найти:
$F_2 - ?$
Решение:
На носилки с листьями действует сила тяжести $\text{P}$, направленная вниз. Она равна:
$P = m \cdot g = 15 \text{ кг} \cdot 10 \frac{\text{Н}}{\text{кг}} = 150 \text{ Н}$.
Ваня и Алиса удерживают носилки, прикладывая силы $F_1$ и $F_2$ соответственно, направленные вверх. Чтобы носилки находились в равновесии, суммарная сила, направленная вверх, должна быть равна силе тяжести, направленной вниз:
$F_1 + F_2 = P$
Отсюда можем найти силу, которую прикладывает Алиса:
$F_2 = P - F_1 = 150 \text{ Н} - 80 \text{ Н} = 70 \text{ Н}$.
Ответ: $F_2 = 70 \text{ Н}$.
№ 4.
Дано:
$F_1 = 250 \text{ Н}$
$F_2 = 150 \text{ Н}$
$F_3 = 100 \text{ Н}$
$F_4 = 35 \text{ Н}$
$F_5 = 14 \text{ Н}$
$F = 550 \text{ Н}$
Найти:
$F_6 - ?$
Решение:
Чтобы вытащить Репку, общая сила, с которой её тянут, должна быть не меньше силы, с которой Репка держится за землю. Все персонажи тянут в одном направлении, поэтому их силы складываются.
Общая сила $F_{общ}$ равна сумме сил всех персонажей:
$F_{общ} = F_1 + F_2 + F_3 + F_4 + F_5 + F_6$
Для того чтобы вытащить репку, должно выполняться условие $F_{общ} \geq F$. Найдём минимальную силу, которую должна приложить Мышка, для этого приравняем общую силу к силе сопротивления Репки:
$F_1 + F_2 + F_3 + F_4 + F_5 + F_6 = F$
Выразим отсюда искомую силу $F_6$:
$F_6 = F - (F_1 + F_2 + F_3 + F_4 + F_5)$
Подставим числовые значения:
$F_6 = 550 \text{ Н} - (250 \text{ Н} + 150 \text{ Н} + 100 \text{ Н} + 35 \text{ Н} + 14 \text{ Н})$
$F_6 = 550 \text{ Н} - 549 \text{ Н} = 1 \text{ Н}$.
Ответ: $F_6 = 1 \text{ Н}$.
№ 5.
Дано:
$\rho = 7,3 \frac{\text{г}}{\text{см}^3}$
$a = 3,0 \text{ см}$
$g = 10 \frac{\text{Н}}{\text{кг}}$
$ \rho = 7,3 \frac{\text{г}}{\text{см}^3} = 7,3 \cdot \frac{0,001 \text{ кг}}{(0,01 \text{ м})^3} = 7,3 \cdot \frac{10^{-3}}{10^{-6}} \frac{\text{кг}}{\text{м}^3} = 7300 \frac{\text{кг}}{\text{м}^3} $
$ a = 3,0 \text{ см} = 0,03 \text{ м} $
Найти:
$F_{упр} - ?$
Решение:
Кубик лежит на столе, следовательно, он находится в состоянии покоя. Сила упругости $F_{упр}$, действующая на кубик со стороны стола, уравновешивает силу тяжести $F_{тяж}$, действующую на кубик. Сила упругости направлена вверх, а сила тяжести — вниз.
$F_{упр} = F_{тяж}$
Силу тяжести можно найти по формуле $F_{тяж} = m \cdot g$, где $\text{m}$ — масса кубика.
Массу кубика найдем через его плотность $\rho$ и объем $\text{V}$: $m = \rho \cdot V$.
Объем кубика равен $V = a^3$.
Соберем все формулы вместе: $F_{упр} = \rho \cdot a^3 \cdot g$.
Подставим значения в системе СИ:
$F_{упр} = 7300 \frac{\text{кг}}{\text{м}^3} \cdot (0,03 \text{ м})^3 \cdot 10 \frac{\text{Н}}{\text{кг}}$
$F_{упр} = 7300 \cdot 0,000027 \cdot 10 \text{ Н} = 0,1971 \cdot 10 \text{ Н} = 1,971 \text{ Н}$.
Ответ: $F_{упр} = 1,971 \text{ Н}$.
№ 6.
Дано:
$m = 1,5 \text{ т}$
$F_{дв} = \frac{1}{3} F_{упр}$
$g = 10 \frac{\text{Н}}{\text{кг}}$
Движение равномерное.
$ m = 1,5 \text{ т} = 1500 \text{ кг} $
Найти:
$F_{сопр} - ?$
Решение:
Поскольку автомобиль движется по горизонтальной трассе, сила упругости (реакции опоры) $F_{упр}$ уравновешивает силу тяжести $F_{тяж}$:
$F_{упр} = F_{тяж} = m \cdot g$
$F_{упр} = 1500 \text{ кг} \cdot 10 \frac{\text{Н}}{\text{кг}} = 15000 \text{ Н}$.
По условию задачи, сила двигателя $F_{дв}$ в 3 раза меньше силы упругости:
$F_{дв} = \frac{1}{3} F_{упр} = \frac{1}{3} \cdot 15000 \text{ Н} = 5000 \text{ Н}$.
Автомобиль движется равномерно, значит, по первому закону Ньютона, равнодействующая всех сил, действующих на него, равна нулю. В горизонтальном направлении на автомобиль действуют сила двигателя $F_{дв}$ и сила сопротивления $F_{сопр}$. Они направлены в противоположные стороны и равны по модулю:
$F_{сопр} = F_{дв} = 5000 \text{ Н}$.
Переведем ответ в килоньютоны:
$F_{сопр} = 5000 \text{ Н} = 5 \text{ кН}$.
Подтверждение рисунком: На автомобиль действуют четыре силы. Вертикально вниз — сила тяжести $F_{тяж} = 15000 \text{ Н}$. Вертикально вверх — сила упругости $F_{упр} = 15000 \text{ Н}$. Горизонтально вперед — сила двигателя $F_{дв} = 5000 \text{ Н}$. Горизонтально назад — сила сопротивления $F_{сопр} = 5000 \text{ Н}$. Пары сил (вертикальных и горизонтальных) равны по модулю и противоположны по направлению, их векторная сумма равна нулю.
Ответ: $F_{сопр} = 5 \text{ кН}$.
Другие задания:
Помогло решение? Оставьте отзыв в комментариях ниже.
Присоединяйтесь к Телеграм-группе @gdz_by_belarus
ПрисоединитьсяМы подготовили для вас ответ c подробным объяснением домашего задания по физике за 7 класс, для упражнения номер 2 расположенного на странице 64 к обучающей тетради 2021 года издания для учащихся школ и гимназий.
Теперь на нашем сайте ГДЗ.ТОП вы всегда легко и бесплатно найдёте условие с правильным ответом на вопрос «Как решить ДЗ» и «Как сделать» задание по физике к упражнению №2 (с. 64), авторов: Шабусов (Анатолий Константинович), Дубина (Максим Викторович), Батурчик (Борис Петрович), учебного пособия издательства Новое знание.













