Номер 10, страница 91 - гдз по физике 8 класс самостоятельные и контрольные работы Шабусов, Дубина

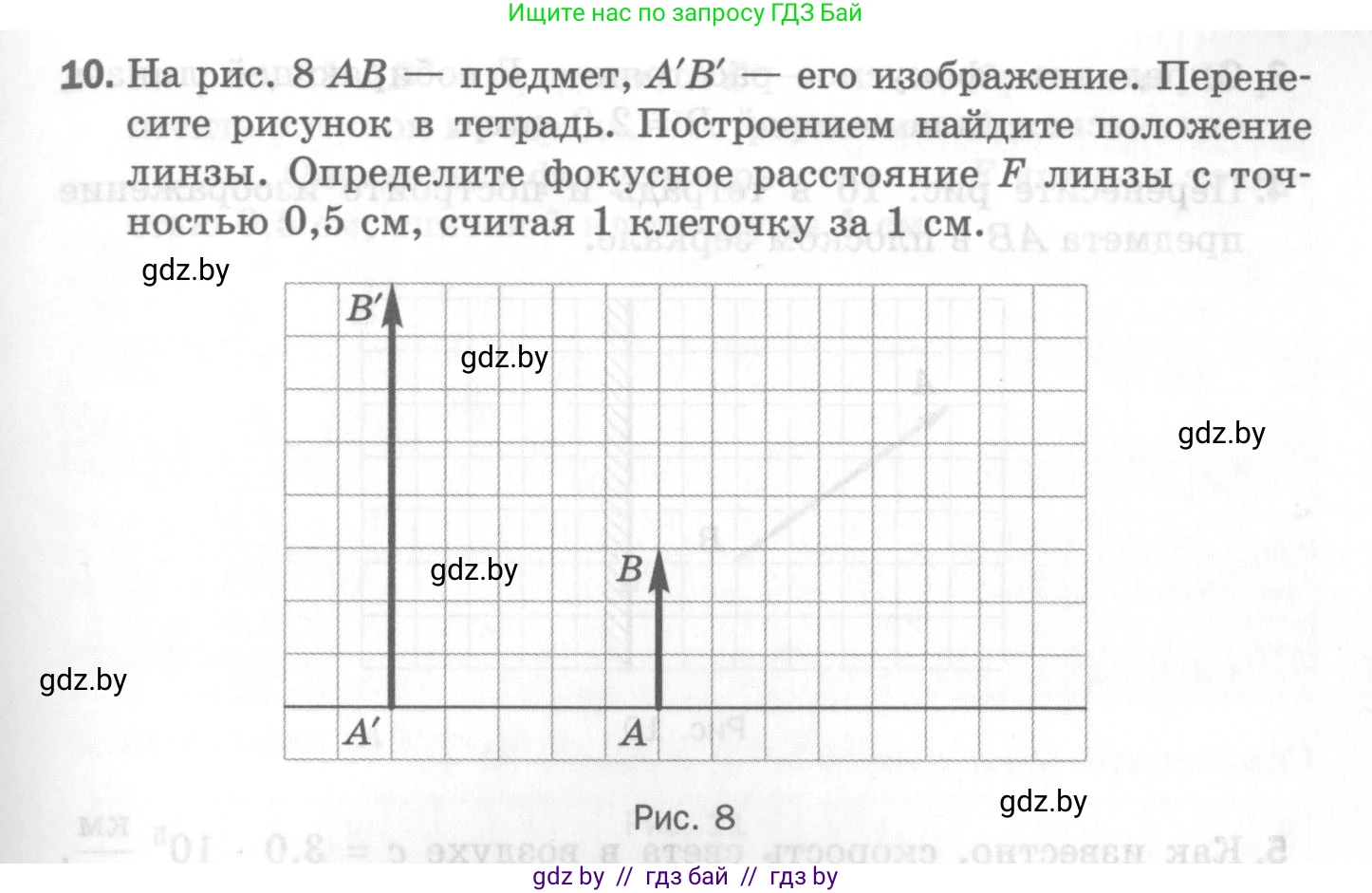
10. На рис. 8 $\text{AB}$ — предмет, $A'B'$ — его изображение. Перенесите рисунок в тетрадь. Построением найдите положение линзы. Определите фокусное расстояние $\text{F}$ линзы с точностью 0,5 см, считая 1 клеточку за 1 см.

Рис. 8

Дано:

Изображение предмета AB и его мнимого изображения A'B' в линзе (Рис. 8).

Масштаб: 1 клеточка = 1 см.

Высота предмета $h = AB = 2$ клеточки = 2 см.

Высота изображения $H = A'B' = 4$ клеточки = 4 см.

Расстояние между основаниями предмета и изображения $AA' = 3$ клеточки = 3 см.

Перевод в СИ:

$h = 0.02$ м.

$H = 0.04$ м.

$AA' = 0.03$ м.

Найти:

Положение линзы.

Фокусное расстояние линзы F.

Решение:

Из рисунка видно, что изображение A'B' является прямым (неперевернутым) и увеличенным по сравнению с предметом AB ($H > h$). Такое изображение дает собирающая линза, когда предмет находится между линзой и ее фокусом. Изображение при этом является мнимым.

Нахождение положения линзы построением

Чтобы найти положение линзы, воспользуемся свойством луча, проходящего через оптический центр линзы: такой луч не меняет своего направления. Это означает, что вершина предмета (точка B), вершина изображения (точка B') и оптический центр линзы (точка O) лежат на одной прямой. Главная оптическая ось линзы — это прямая, на которой лежат основания предмета и изображения (прямая AA').

Таким образом, для нахождения положения линзы необходимо провести прямую через точки B и B'. Точка пересечения этой прямой с главной оптической осью AA' и будет являться оптическим центром O, в котором расположена линза.

Для точного определения положения линзы воспользуемся методом подобия треугольников. Пусть $\text{d}$ — расстояние от предмета до линзы, а $\text{f}$ — расстояние от изображения до линзы. Из подобия треугольников, образованных высотами предмета и изображения и главной оптической осью, следует, что линейное увеличение линзы $\Gamma$ равно:

$\Gamma = \frac{H}{h} = \frac{f}{d}$

Подставим известные значения: $\Gamma = \frac{4 \text{ см}}{2 \text{ см}} = 2$.

Следовательно, $f/d = 2$, или $f = 2d$.

Из рисунка видно, что расстояние между предметом и изображением равно 3 см. Так как изображение мнимое, и предмет, и изображение находятся по одну сторону от линзы. При этом предмет расположен между изображением и линзой. Расстояние между ними равно разности расстояний до линзы: $f - d = 3 \text{ см}$.

Решим систему уравнений:

$\begin{cases} f = 2d \\ f - d = 3 \end{cases}$

Подставив первое уравнение во второе, получим: $2d - d = 3$, откуда $d = 3 \text{ см}$.

Тогда расстояние до изображения $f = 2 \cdot 3 = 6 \text{ см}$.

Итак, линза находится на расстоянии 3 см от предмета AB (справа от него на рисунке) и на расстоянии 6 см от изображения A'B'.

Определение фокусного расстояния F линзы

Для определения фокусного расстояния F построим ход луча, идущего от вершины предмета B параллельно главной оптической оси. После преломления в линзе этот луч (а в случае мнимого изображения — его продолжение в обратную сторону) пройдет через фокус линзы.

Построение:

1. Из точки B проводим луч, параллельный главной оптической оси, до пересечения с плоскостью линзы в некоторой точке P.
2. Поскольку мы знаем, где находится мнимое изображение B', преломленный луч должен идти так, как будто он исходит из точки B'. Поэтому соединяем точку P с точкой B' и продолжаем эту прямую до пересечения с главной оптической осью.
3. Точка пересечения F' этой прямой с главной оптической осью и есть задний главный фокус линзы.
4. Расстояние от оптического центра O до фокуса F' и есть искомое фокусное расстояние F.

Для точного расчета используем формулу тонкой линзы. Для собирающей линзы, дающей мнимое изображение, она имеет вид:

$\frac{1}{F} = \frac{1}{d} - \frac{1}{f}$

Подставим найденные ранее значения $d = 3$ см и $f = 6$ см:

$\frac{1}{F} = \frac{1}{3} - \frac{1}{6}$

Приводя к общему знаменателю:

$\frac{1}{F} = \frac{2}{6} - \frac{1}{6} = \frac{1}{6}$

Отсюда находим фокусное расстояние:

$F = 6$ см.

Ответ:

Линза является собирающей и расположена на расстоянии 3 см от предмета и 6 см от изображения. Фокусное расстояние линзы $F = 6$ см.