Номер 2, страница 28 - гдз по физике 7 класс обучающая тетрадь Шабусов, Дубина

Авторы: Шабусов А. К., Дубина М. В., Батурчик Б. П.
Тип: обучающая тетрадь
Издательство: Новое знание
Год издания: 2021 - 2026
Цвет обложки: жёлтый
ISBN: 978-985-24-0247-7
Популярные ГДЗ в 7 классе
Урок 19. Решение задач по теме «Равномерное прямолинейное движение. Скорость» - номер 2, страница 28.
№2 (с. 28)
Условие. №2 (с. 28)
скриншот условия


2. Учимся решать задачи.
№ 1. Алиса на велосипеде преодолела путь $s = 440$ м с постоянной скоростью $v = 8,0 \frac{\text{м}}{\text{с}}$. Определите время $\Delta t$ движения Алисы.
Заполните матрицу.
| Дано: | Решение |
| $s = \text{\_\_\_\_\_\_ }$ М | $v = \frac{s}{\Delta t}$; $\Delta t = \frac{s}{v}$ |
| $v = \text{\_\_\_\_\_\_ } \frac{\text{м}}{\text{с}}$ | $\Delta t = \frac{\text{\_\_\_\_\_\_ }\text{м}}{\text{\_\_\_\_\_\_ }\frac{\text{м}}{\text{с}}} = \text{\_\_\_\_\_\_ }$ c |
| $\Delta t - ?$ |
Ответ: $\Delta t = \text{\_\_\_\_\_\_ }$ c.
№ 2. Алиса шла $\Delta t = 12$ мин с постоянной скоростью $v = 1,4 \frac{\text{м}}{\text{с}}$. Определите путь $\text{s}$, который прошла Алиса.
| Дано: | Решение |
| $\Delta t = 12$ мин $= 720$ с | $v = \frac{s}{\Delta t}$; $s = v\Delta t$ |
| $v = \text{\_\_\_\_\_\_ } \frac{\text{м}}{\text{с}}$ | $s = \text{\_\_\_\_\_\_ }\frac{\text{м}}{\text{с}} \cdot 720 \text{ с} = \text{\_\_\_\_\_\_ }$ м $= \text{\_\_\_\_\_\_ }$ км. |
| $s - ?$ |
Ответ: $s = \text{\_\_\_\_\_\_ }$ км.
№ 3. (задача с комментариями). Алиса и Ваня во время перемены стояли на коридоре. Когда прозвенел звонок, ребята поспешили на уроки: Алиса пошла направо со скоростью $v_1 = 1,7 \frac{\text{м}}{\text{с}}$, а Ваня — налево со скоростью $v_2 = 1,3 \frac{\text{м}}{\text{с}}$. Какое расстояние $\text{s}$ станет между Алисой и Ваней через $\Delta t = 4,0$ с после звонка? Движение Алисы и Вани за это время считайте равномерным и прямолинейным.
| Дано: | Решение |
| $v_1 = \text{\_\_\_\_\_\_ } \frac{\text{м}}{\text{с}}$ | Расстояние между Алисой и Ваней равно сумме путей, которые они пройдут: |
| $v_2 = \text{\_\_\_\_\_\_ } \frac{\text{м}}{\text{с}}$ | |
| $\Delta t = \text{\_\_\_\_\_\_ }$ c | $s = s_1 + s_2$. |
| $s - ?$ | Дальше решаем по алгоритму предыдущей задачи: |
| $s_1 = v_1\Delta t$; $s_2 = \text{\_\_\_\_\_\_ } \cdot \text{\_\_\_\_\_\_ }$ |
Можно рассчитать пути по отдельности, а можно всё свести в одну формулу:
$s = v_1\Delta t + v_2\Delta t$.
Вынесем $\Delta t$ за скобки:
$s = (v_1 + v_2)\Delta t$.
Подставим значения в формулу и произведем вычисления:
$s = (\text{\_\_\_\_\_\_ }\frac{\text{м}}{\text{с}} + \text{\_\_\_\_\_\_ }\frac{\text{м}}{\text{с}}) \cdot \text{\_\_\_\_\_\_ }\text{ с} = \text{\_\_\_\_\_\_ }$ М.
Ответ: $s = \text{\_\_\_\_\_\_ }$ М.
№ 4. Алиса, Ваня и кот Маркиз устроили соревнование. Алиса бежала со скоростью $v_1 = 18 \frac{\text{км}}{\text{ч}}$, скорость Вани $v_2 = 5,5 \frac{\text{м}}{\text{с}}$, а кот Маркиз развил скорость $v_3 = 270$ м/мин. Определите, как распределились места среди бегунов, если все бежали с постоянной скоростью.
№ 5. Алиса шла со скоростью $v = 3,6 \frac{\text{км}}{\text{ч}}$ промежуток времени $\Delta t = 15$ мин. Определите путь $\text{s}$, который прошла Алиса.
| Дано: | Решение |
| $\Delta t = \text{\_\_\_\_\_\_ }$ мин $= \text{\_\_\_\_\_\_ }$ c | $v = \frac{s}{\Delta t}$; $s = v\Delta t$ |
| $v = \text{\_\_\_\_\_\_ }\frac{\text{км}}{\text{ч}} = \text{\_\_\_\_\_\_ }\frac{\text{м}}{\text{с}}$ | $s = \text{\_\_\_\_\_\_ }\frac{\text{м}}{\text{с}} \cdot \text{\_\_\_\_\_\_ }\text{ с} = \text{\_\_\_\_\_\_ }$ м. |
| $s - ?$ |
Ответ: $s = \text{\_\_\_\_\_\_ }$ м.
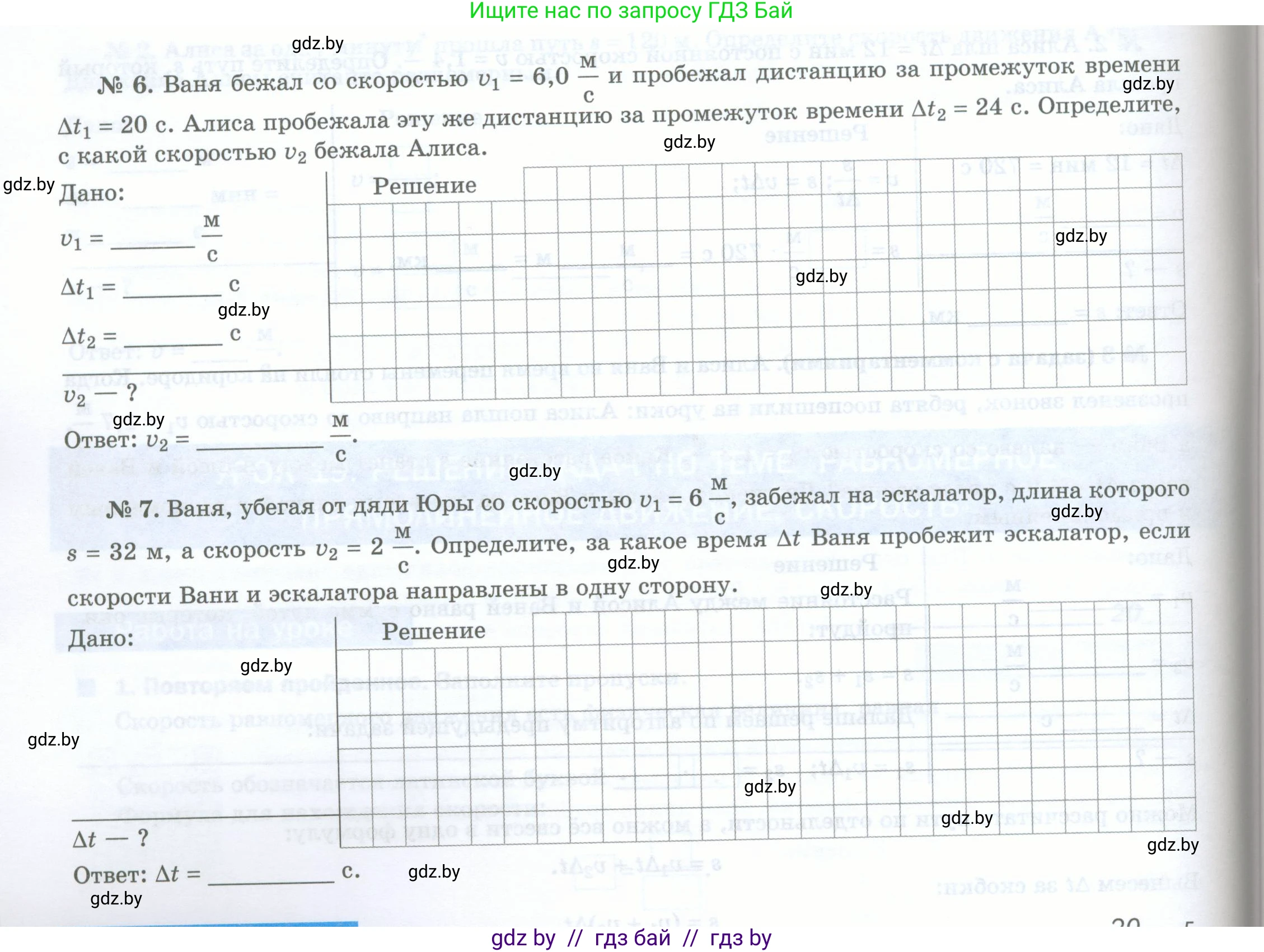
№ 6. Ваня бежал со скоростью $v_1 = 6,0 \frac{\text{м}}{\text{с}}$ и пробежал дистанцию за промежуток времени $\Delta t_1 = 20$ с. Алиса пробежала эту же дистанцию за промежуток времени $\Delta t_2 = 24$ с. Определите, с какой скоростью $v_2$ бежала Алиса.
| Дано: | Решение |
| $v_1 = \text{\_\_\_\_\_\_ } \frac{\text{м}}{\text{с}}$ | |
| $\Delta t_1 = \text{\_\_\_\_\_\_ }$ c | |
| $\Delta t_2 = \text{\_\_\_\_\_\_ }$ c | |
| $v_2 - ?$ |
Ответ: $v_2 = \text{\_\_\_\_\_\_ }\frac{\text{м}}{\text{с}}$.
№ 7. Ваня, убегая от дяди Юры со скоростью $v_1 = 6 \frac{\text{м}}{\text{с}}$, забежал на эскалатор, длина которого $s = 32$ м, а скорость $v_2 = 2 \frac{\text{м}}{\text{с}}$. Определите, за какое время $\Delta t$ Ваня пробежит эскалатор, если скорости Вани и эскалатора направлены в одну сторону.
| Дано: | Решение |
| $\Delta t - ?$ |
Ответ: $\Delta t = \text{\_\_\_\_\_\_ }$ c.
Ршение. №2 (с. 28)
№ 1.
Дано:
$s = 440$ м
$v = 8,0 \frac{м}{с}$
Найти:
$\Delta t$ - ?
Решение:
Скорость при равномерном прямолинейном движении находится по формуле $v = \frac{s}{\Delta t}$.
Чтобы найти время движения $\Delta t$, выразим его из этой формулы: $\Delta t = \frac{s}{v}$.
Подставим заданные значения в формулу:
$\Delta t = \frac{440 \text{ м}}{8,0 \frac{м}{с}} = 55 \text{ с}$.
Ответ: $\Delta t = 55$ с.
№ 2.
Дано:
$\Delta t = 12$ мин
$v = 1,4 \frac{м}{с}$
Переведем время в систему СИ:
$\Delta t = 12 \text{ мин} = 12 \cdot 60 \text{ с} = 720 \text{ с}$.
Найти:
$\text{s}$ - ?
Решение:
Путь при равномерном движении находится по формуле $s = v \cdot \Delta t$.
Подставим значения:
$s = 1,4 \frac{м}{с} \cdot 720 \text{ с} = 1008 \text{ м}$.
Для ответа переведем метры в километры: $1008 \text{ м} = 1,008 \text{ км}$.
Ответ: $s = 1,008$ км.
№ 3.
Дано:
$v_1 = 1,7 \frac{м}{с}$
$v_2 = 1,3 \frac{м}{с}$
$\Delta t = 4,0$ с
Найти:
$\text{s}$ - ?
Решение:
Алиса и Ваня движутся в противоположных направлениях. Расстояние между ними будет равно сумме путей, пройденных каждым из них за время $\Delta t$: $s = s_1 + s_2$.
Пути, пройденные Алисой ($s_1$) и Ваней ($s_2$), равны:
$s_1 = v_1 \Delta t$
$s_2 = v_2 \Delta t$
Таким образом, общее расстояние можно найти по формуле $s = (v_1 + v_2) \Delta t$.
Подставим числовые значения:
$s = (1,7 \frac{м}{с} + 1,3 \frac{м}{с}) \cdot 4,0 \text{ с} = 3,0 \frac{м}{с} \cdot 4,0 \text{ с} = 12 \text{ м}$.
Ответ: $s = 12$ м.
№ 4.
Дано:
Скорость Алисы $v_1 = 18 \frac{км}{ч}$
Скорость Вани $v_2 = 5,5 \frac{м}{с}$
Скорость кота Маркиза $v_3 = 270 \frac{м}{мин}$
Найти:
Распределение мест.
Решение:
Чтобы сравнить скорости, необходимо привести их к единой единице измерения, например, к метрам в секунду (м/с).
1. Скорость Алисы: $v_1 = 18 \frac{км}{ч} = 18 \cdot \frac{1000 \text{ м}}{3600 \text{ с}} = 5 \frac{м}{с}$.
2. Скорость Вани: $v_2 = 5,5 \frac{м}{с}$.
3. Скорость кота Маркиза: $v_3 = 270 \frac{м}{мин} = \frac{270 \text{ м}}{60 \text{ с}} = 4,5 \frac{м}{с}$.
Теперь сравним полученные значения: $5,5 \frac{м}{с} > 5 \frac{м}{с} > 4,5 \frac{м}{с}$, следовательно, $v_2 > v_1 > v_3$.
Места распределяются в соответствии со скоростью: чем выше скорость, тем выше место.
1-е место — Ваня
2-е место — Алиса
3-е место — кот Маркиз
Ответ: 1-е место — Ваня, 2-е место — Алиса, 3-е место — кот Маркиз.
№ 5.
Дано:
$v = 3,6 \frac{км}{ч}$
$\Delta t = 15$ мин
Переведем все величины в систему СИ:
$v = 3,6 \frac{км}{ч} = 3,6 \cdot \frac{1000 \text{ м}}{3600 \text{ с}} = 1 \frac{м}{с}$.
$\Delta t = 15 \text{ мин} = 15 \cdot 60 \text{ с} = 900 \text{ с}$.
Найти:
$\text{s}$ - ?
Решение:
Для нахождения пути используем формулу $s = v \cdot \Delta t$.
Подставим значения в СИ:
$s = 1 \frac{м}{с} \cdot 900 \text{ с} = 900 \text{ м}$.
Ответ: $s = 900$ м.
№ 6.
Дано:
$v_1 = 6,0 \frac{м}{с}$ (скорость Вани)
$\Delta t_1 = 20$ с (время Вани)
$\Delta t_2 = 24$ с (время Алисы)
Найти:
$v_2$ - ? (скорость Алисы)
Решение:
Ваня и Алиса пробежали одинаковую дистанцию $\text{s}$. Сначала определим эту дистанцию по данным Вани: $s = v_1 \cdot \Delta t_1$.
$s = 6,0 \frac{м}{с} \cdot 20 \text{ с} = 120 \text{ м}$.
Теперь, зная дистанцию и время Алисы, найдем ее скорость: $v_2 = \frac{s}{\Delta t_2}$.
$v_2 = \frac{120 \text{ м}}{24 \text{ с}} = 5 \frac{м}{с}$.
Ответ: $v_2 = 5 \frac{м}{с}$.
№ 7.
Дано:
$v_1 = 6 \frac{м}{с}$ (скорость Вани)
$v_2 = 2 \frac{м}{с}$ (скорость эскалатора)
$s = 32$ м (длина эскалатора)
Найти:
$\Delta t$ - ?
Решение:
Так как Ваня и эскалатор движутся в одном направлении, их скорости складываются. Результирующая скорость Вани относительно земли равна $v_{общ} = v_1 + v_2$.
$v_{общ} = 6 \frac{м}{с} + 2 \frac{м}{с} = 8 \frac{м}{с}$.
Время, за которое Ваня преодолеет эскалатор, найдем по формуле $\Delta t = \frac{s}{v_{общ}}$.
$\Delta t = \frac{32 \text{ м}}{8 \frac{м}{с}} = 4 \text{ с}$.
Ответ: $\Delta t = 4$ с.
Другие задания:
Помогло решение? Оставьте отзыв в комментариях ниже.
Присоединяйтесь к Телеграм-группе @gdz_by_belarus
ПрисоединитьсяМы подготовили для вас ответ c подробным объяснением домашего задания по физике за 7 класс, для упражнения номер 2 расположенного на странице 28 к обучающей тетради 2021 года издания для учащихся школ и гимназий.
Теперь на нашем сайте ГДЗ.ТОП вы всегда легко и бесплатно найдёте условие с правильным ответом на вопрос «Как решить ДЗ» и «Как сделать» задание по физике к упражнению №2 (с. 28), авторов: Шабусов (Анатолий Константинович), Дубина (Максим Викторович), Батурчик (Борис Петрович), учебного пособия издательства Новое знание.













