Номер 2, страница 39 - гдз по физике 7 класс обучающая тетрадь Шабусов, Дубина

Авторы: Шабусов А. К., Дубина М. В., Батурчик Б. П.
Тип: обучающая тетрадь
Издательство: Новое знание
Год издания: 2021 - 2026
Цвет обложки: жёлтый
ISBN: 978-985-24-0247-7
Популярные ГДЗ в 7 классе
Урок 24. Решение задач по теме «Неравномерное движение. Средняя скорость». Работа на уроке - номер 2, страница 39.
№2 (с. 39)
Условие. №2 (с. 39)
скриншот условия
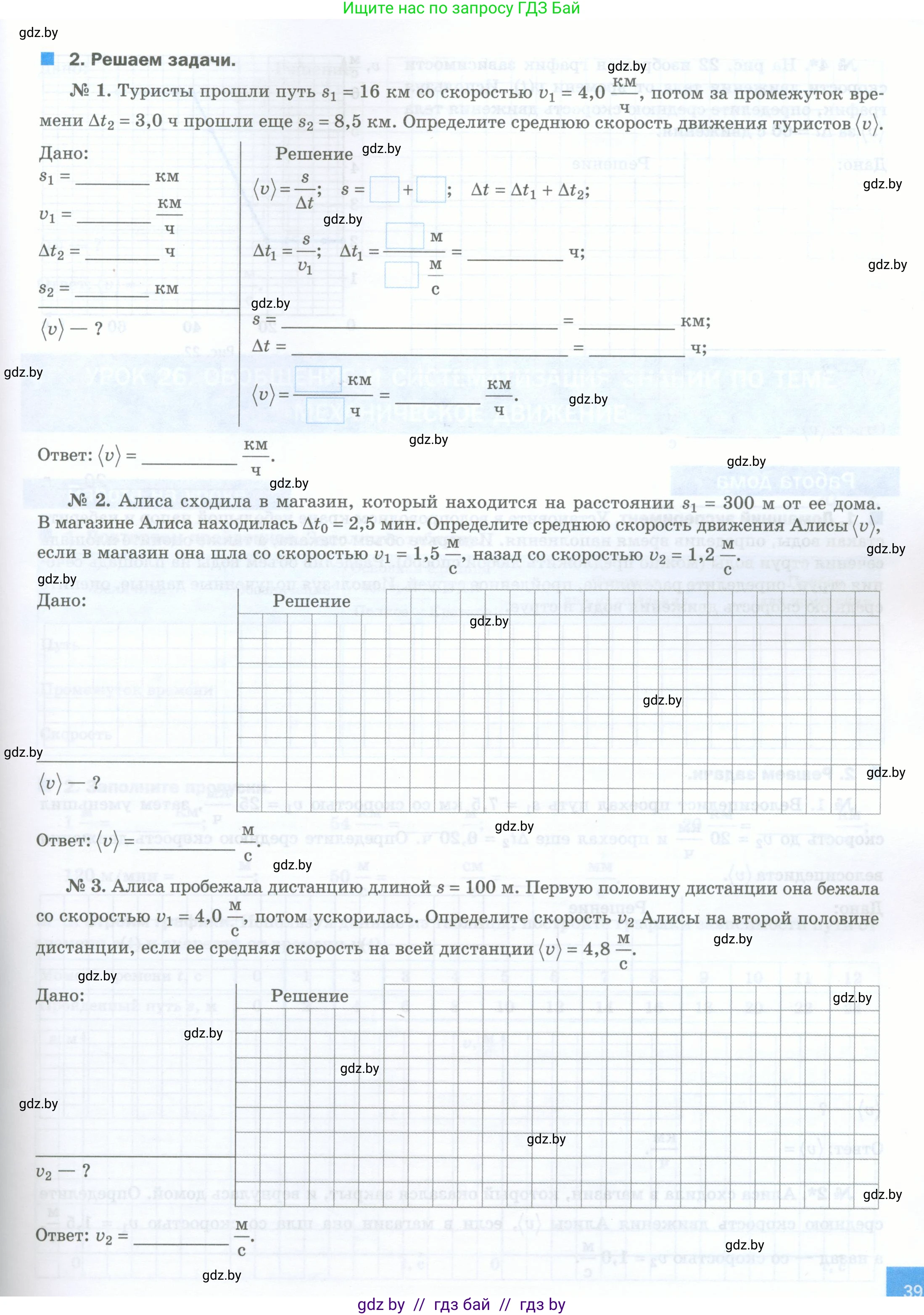
2. Решаем задачи.
№ 1. Туристы прошли путь $s_1 = 16$ км со скоростью $v_1 = 4,0 \frac{\text{км}}{\text{ч}}$, потом за промежуток времени $\Delta t_2 = 3,0$ ч прошли еще $s_2 = 8,5$ км. Определите среднюю скорость движения туристов $\langle v \rangle$.
| Дано: | Решение: |
| $s_1 = \_\_\_\_$ км | $\langle v \rangle = \frac{s}{\Delta t}$; $s = \_\_\_\_ + \_\_\_\_$; $\Delta t = \Delta t_1 + \Delta t_2$; |
| $v_1 = \_\_\_\_ \frac{\text{км}}{\text{ч}}$ | $\Delta t_1 = \frac{s_1}{v_1} = \frac{\_\_\_\text{M}}{\_\_\_\text{c}} = \_\_\_\_$ ч; |
| $\Delta t_2 = \_\_\_\_$ ч | $s = \_\_\_\_$ км; |
| $s_2 = \_\_\_\_$ км | $\Delta t = \_\_\_\_$ ч; |
| $\langle v \rangle - ?$ | $\langle v \rangle = \frac{\_\_\_\text{KM}}{\_\_\_\text{ч}} = \frac{\_\_\_\text{KM}}{\_\_\_\text{ч}}$. |
Ответ: $\langle v \rangle = \_\_\_\_ \frac{\text{км}}{\text{ч}}$.
№ 2. Алиса сходила в магазин, который находится на расстоянии $s_1 = 300$ м от ее дома. В магазине Алиса находилась $\Delta t_0 = 2,5$ мин. Определите среднюю скорость движения Алисы $\langle v \rangle$, если в магазин она шла со скоростью $v_1 = 1,5 \frac{\text{м}}{\text{с}}$, назад со скоростью $v_2 = 1,2 \frac{\text{м}}{\text{с}}$.
| Дано: | Решение: |
$\langle v \rangle - ?$
Ответ: $\langle v \rangle = \_\_\_\_ \frac{\text{м}}{\text{с}}$.
№ 3. Алиса пробежала дистанцию длиной $s = 100$ м. Первую половину дистанции она бежала со скоростью $v_1 = 4,0 \frac{\text{м}}{\text{с}}$, потом ускорилась. Определите скорость $v_2$ Алисы на второй половине дистанции, если ее средняя скорость на всей дистанции $\langle v \rangle = 4,8 \frac{\text{м}}{\text{с}}$.
| Дано: | Решение: |
$v_2 - ?$
Ответ: $v_2 = \_\_\_\_ \frac{\text{м}}{\text{с}}$.
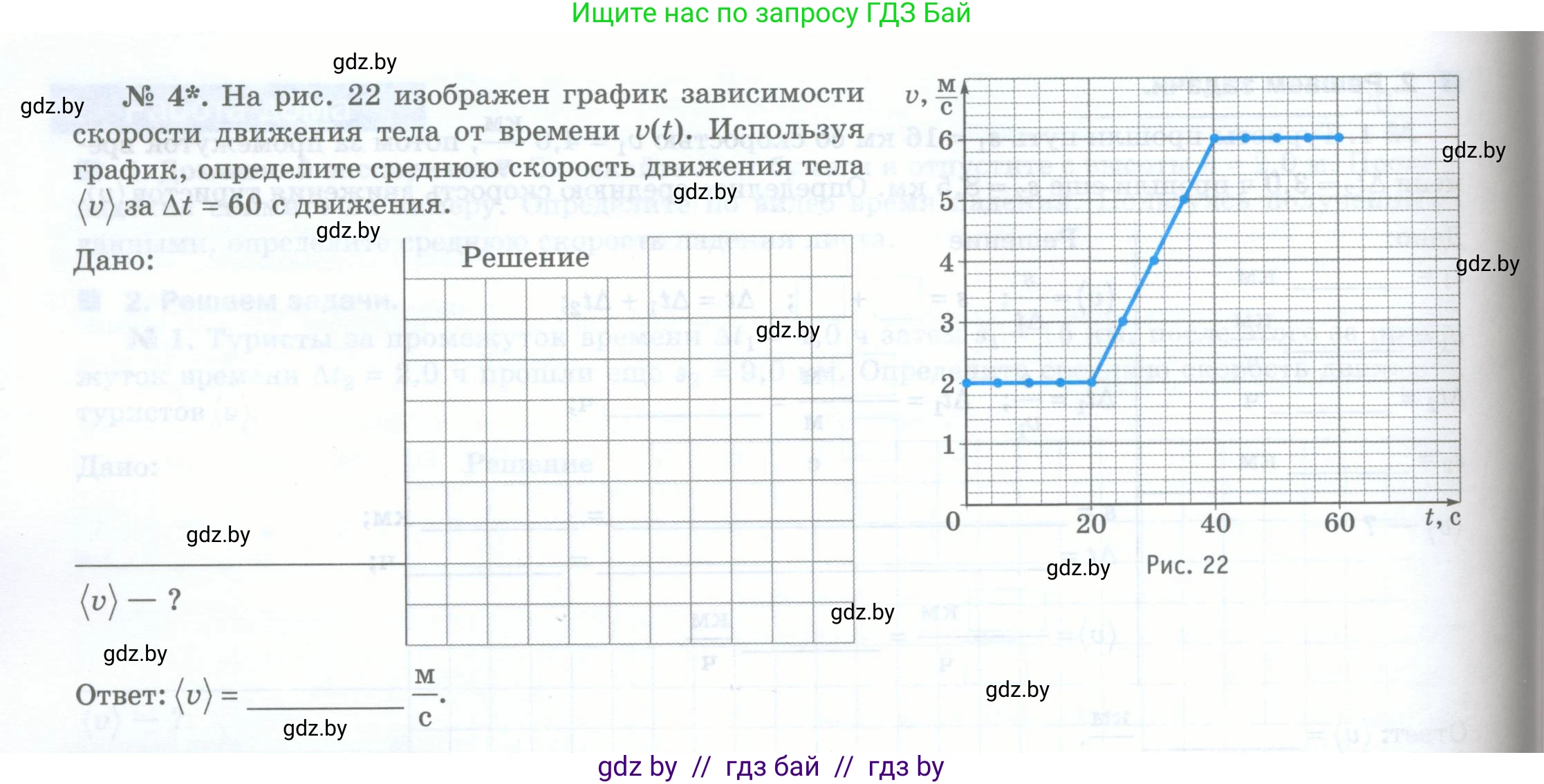
№ 4*. На рис. 22 изображен график зависимости скорости движения тела от времени $v(t)$. Используя график, определите среднюю скорость движения тела $\langle v \rangle$ за $\Delta t = 60$ с движения.
| Дано: | Решение: |
$\langle v \rangle - ?$
Ответ: $\langle v \rangle = \_\_\_\_ \frac{\text{м}}{\text{с}}$.
Рис. 22
Ршение. №2 (с. 39)
№ 1.
Дано:
$s_1 = 16$ км
$v_1 = 4,0$ км/ч
$\Delta t_2 = 3,0$ ч
$s_2 = 8,5$ км
Найти:
$\langle v \rangle$ - ?
Решение:
Средняя скорость определяется как отношение всего пройденного пути ко всему времени движения:
$\langle v \rangle = \frac{s}{\Delta t}$
Найдем общий путь $\text{s}$ и общее время $\Delta t$.
Общий путь: $s = s_1 + s_2 = 16 \text{ км} + 8,5 \text{ км} = 24,5$ км.
Время движения на первом участке: $\Delta t_1 = \frac{s_1}{v_1} = \frac{16 \text{ км}}{4,0 \text{ км/ч}} = 4,0$ ч.
Общее время движения: $\Delta t = \Delta t_1 + \Delta t_2 = 4,0 \text{ ч} + 3,0 \text{ ч} = 7,0$ ч.
Теперь можем рассчитать среднюю скорость:
$\langle v \rangle = \frac{s}{\Delta t} = \frac{24,5 \text{ км}}{7,0 \text{ ч}} = 3,5$ км/ч.
Ответ: $\langle v \rangle = 3,5$ км/ч.
№ 2.
Дано:
$s_1 = 300$ м
$\Delta t_0 = 2,5$ мин
$v_1 = 1,5$ м/с
$v_2 = 1,2$ м/с
Перевод в СИ:
$\Delta t_0 = 2,5 \text{ мин} = 2,5 \cdot 60 \text{ с} = 150$ с
Найти:
$\langle v \rangle$ - ?
Решение:
Средняя скорость движения определяется как отношение всего пройденного пути ко всему времени, затраченному на этот путь, включая остановки.
$\langle v \rangle = \frac{s_{общ}}{\Delta t_{общ}}$
Алиса прошла путь до магазина $s_1 = 300$ м и обратно такой же путь $s_2 = 300$ м. Общий путь:
$s_{общ} = s_1 + s_2 = 300 \text{ м} + 300 \text{ м} = 600$ м.
Общее время состоит из времени пути до магазина ($\Delta t_1$), времени в магазине ($\Delta t_0$) и времени пути обратно ($\Delta t_2$).
Время пути до магазина: $\Delta t_1 = \frac{s_1}{v_1} = \frac{300 \text{ м}}{1,5 \text{ м/с}} = 200$ с.
Время пути обратно: $\Delta t_2 = \frac{s_1}{v_2} = \frac{300 \text{ м}}{1,2 \text{ м/с}} = 250$ с.
Общее время: $\Delta t_{общ} = \Delta t_1 + \Delta t_0 + \Delta t_2 = 200 \text{ с} + 150 \text{ с} + 250 \text{ с} = 600$ с.
Теперь рассчитаем среднюю скорость:
$\langle v \rangle = \frac{s_{общ}}{\Delta t_{общ}} = \frac{600 \text{ м}}{600 \text{ с}} = 1,0$ м/с.
Ответ: $\langle v \rangle = 1,0$ м/с.
№ 3.
Дано:
$s = 100$ м
$v_1 = 4,0$ м/с (на первой половине пути)
$\langle v \rangle = 4,8$ м/с
Найти:
$v_2$ - ?
Решение:
Средняя скорость на всей дистанции равна отношению всей дистанции ко всему времени движения:
$\langle v \rangle = \frac{s}{\Delta t_{общ}}$
Общее время движения $\Delta t_{общ}$ можно найти из этой формулы: $\Delta t_{общ} = \frac{s}{\langle v \rangle}$.
$\Delta t_{общ} = \frac{100 \text{ м}}{4,8 \text{ м/с}} = \frac{1000}{48} \text{ с} = \frac{125}{6}$ с.
Общее время также равно сумме времен на первой ($\Delta t_1$) и второй ($\Delta t_2$) половинах дистанции: $\Delta t_{общ} = \Delta t_1 + \Delta t_2$.
Первая половина дистанции $s_1 = s/2 = 100 \text{ м} / 2 = 50$ м.
Время на первой половине дистанции: $\Delta t_1 = \frac{s_1}{v_1} = \frac{50 \text{ м}}{4,0 \text{ м/с}} = 12,5$ с.
Теперь найдем время на второй половине дистанции:
$\Delta t_2 = \Delta t_{общ} - \Delta t_1 = \frac{125}{6} \text{ с} - 12,5 \text{ с} = \frac{125}{6} \text{ с} - \frac{25}{2} \text{ с} = \frac{125 - 75}{6} \text{ с} = \frac{50}{6} \text{ с} = \frac{25}{3}$ с.
Вторая половина дистанции также равна $s_2 = s/2 = 50$ м.
Скорость на второй половине дистанции: $v_2 = \frac{s_2}{\Delta t_2} = \frac{50 \text{ м}}{\frac{25}{3} \text{ с}} = \frac{50 \cdot 3}{25} \text{ м/с} = 2 \cdot 3 \text{ м/с} = 6,0$ м/с.
Ответ: $v_2 = 6,0$ м/с.
№ 4*.
Дано:
График зависимости скорости от времени $v(t)$.
Общее время движения $\Delta t = 60$ с.
Найти:
$\langle v \rangle$ - ?
Решение:
Средняя скорость движения равна отношению всего пройденного пути ко всему времени движения:
$\langle v \rangle = \frac{s_{общ}}{\Delta t_{общ}}$
Пройденный путь численно равен площади фигуры под графиком скорости $v(t)$. Разобьем всю фигуру на три части, соответствующие трем участкам движения:
1. Участок от $t_0=0$ с до $t_1=20$ с: движение с постоянной скоростью $v_1 = 2$ м/с. Путь $s_1$ равен площади прямоугольника.
$s_1 = v_1 \cdot (t_1 - t_0) = 2 \text{ м/с} \cdot (20 \text{ с} - 0 \text{ с}) = 40$ м.
2. Участок от $t_1=20$ с до $t_2=40$ с: равноускоренное движение. Скорость изменяется от $v_1 = 2$ м/с до $v_2 = 6$ м/с. Путь $s_2$ равен площади трапеции.
$s_2 = \frac{v_1 + v_2}{2} \cdot (t_2 - t_1) = \frac{2 \text{ м/с} + 6 \text{ м/с}}{2} \cdot (40 \text{ с} - 20 \text{ с}) = \frac{8}{2} \text{ м/с} \cdot 20 \text{ с} = 4 \text{ м/с} \cdot 20 \text{ с} = 80$ м.
3. Участок от $t_2=40$ с до $t_3=60$ с: движение с постоянной скоростью $v_2 = 6$ м/с. Путь $s_3$ равен площади прямоугольника.
$s_3 = v_2 \cdot (t_3 - t_2) = 6 \text{ м/с} \cdot (60 \text{ с} - 40 \text{ с}) = 6 \text{ м/с} \cdot 20 \text{ с} = 120$ м.
Общий пройденный путь:
$s_{общ} = s_1 + s_2 + s_3 = 40 \text{ м} + 80 \text{ м} + 120 \text{ м} = 240$ м.
Общее время движения дано: $\Delta t_{общ} = 60$ с.
Средняя скорость:
$\langle v \rangle = \frac{s_{общ}}{\Delta t_{общ}} = \frac{240 \text{ м}}{60 \text{ с}} = 4,0$ м/с.
Ответ: $\langle v \rangle = 4,0$ м/с.
Другие задания:
Помогло решение? Оставьте отзыв в комментариях ниже.
Присоединяйтесь к Телеграм-группе @gdz_by_belarus
ПрисоединитьсяМы подготовили для вас ответ c подробным объяснением домашего задания по физике за 7 класс, для упражнения номер 2 расположенного на странице 39 к обучающей тетради 2021 года издания для учащихся школ и гимназий.
Теперь на нашем сайте ГДЗ.ТОП вы всегда легко и бесплатно найдёте условие с правильным ответом на вопрос «Как решить ДЗ» и «Как сделать» задание по физике к упражнению №2 (с. 39), авторов: Шабусов (Анатолий Константинович), Дубина (Максим Викторович), Батурчик (Борис Петрович), учебного пособия издательства Новое знание.













