Номер 2, страница 34 - гдз по физике 7 класс обучающая тетрадь Шабусов, Дубина

2. Решаем задачи.

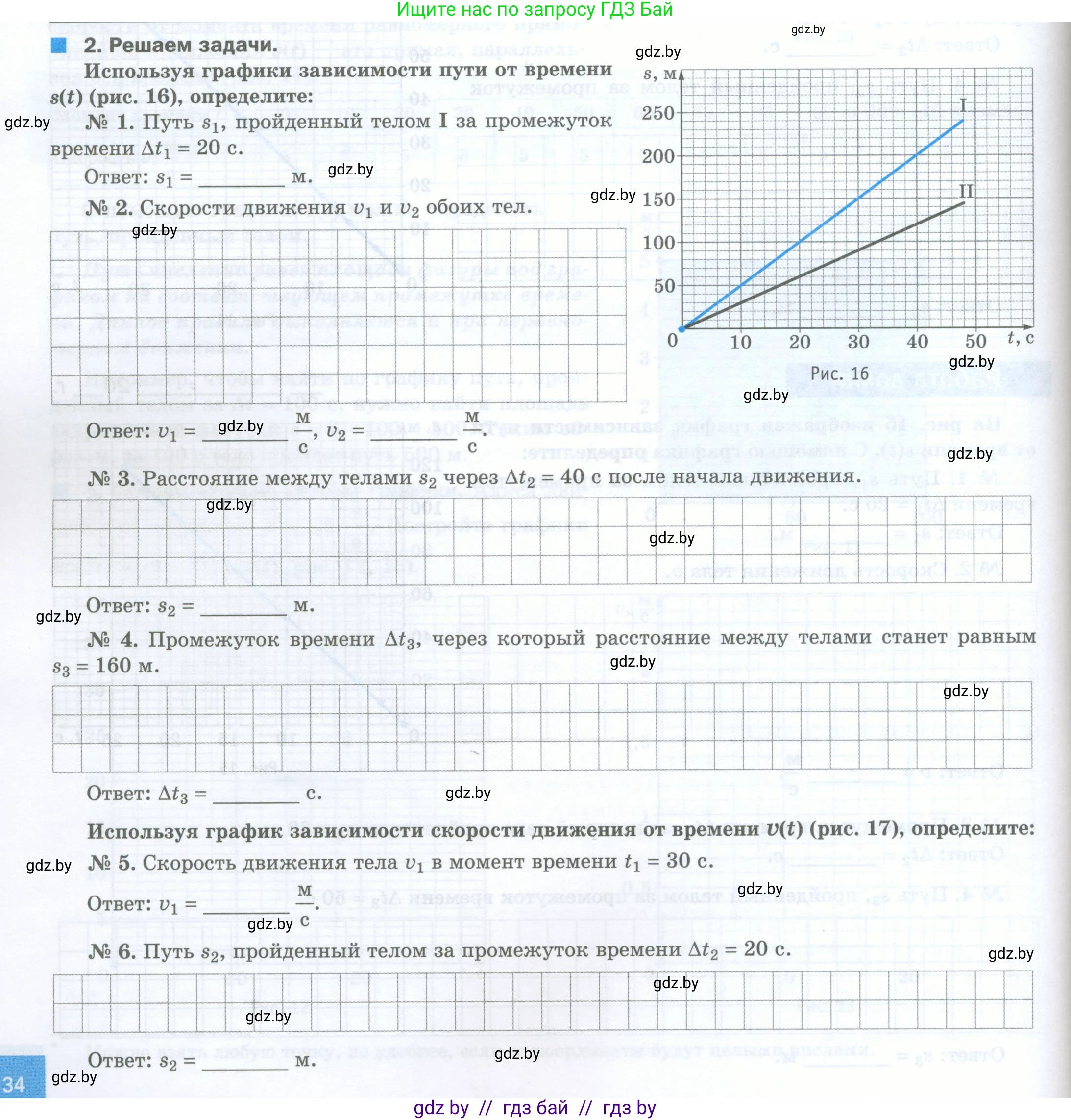
Используя графики зависимости пути от времени $s(t)$ (рис. 16), определите:

№ 1. Путь $s_1$, пройденный телом I за промежуток времени $\Delta t_1 = 20$ с.

Ответ: $s_1 =\text{\_\_\_\_ } м.$

№ 2. Скорости движения $v_1$ и $v_2$ обоих тел.

Ответ: $v_1 = \text{\_\_\_\_\_\_ } \frac{\text{м}}{\text{с}}$, $v_2 = \text{\_\_\_\_\_\_ } \frac{\text{м}}{\text{с}}$

№ 3. Расстояние между телами $s_2$ через $\Delta t_2 = 40$ с после начала движения.

Ответ: $s_2 =\text{\_\_\_\_ } м.$

№ 4. Промежуток времени $\Delta t_3$, через который расстояние между телами станет равным $s_3 = 160$ м.

Ответ: $\Delta t_3 =\text{\_\_\_\_ } с.$

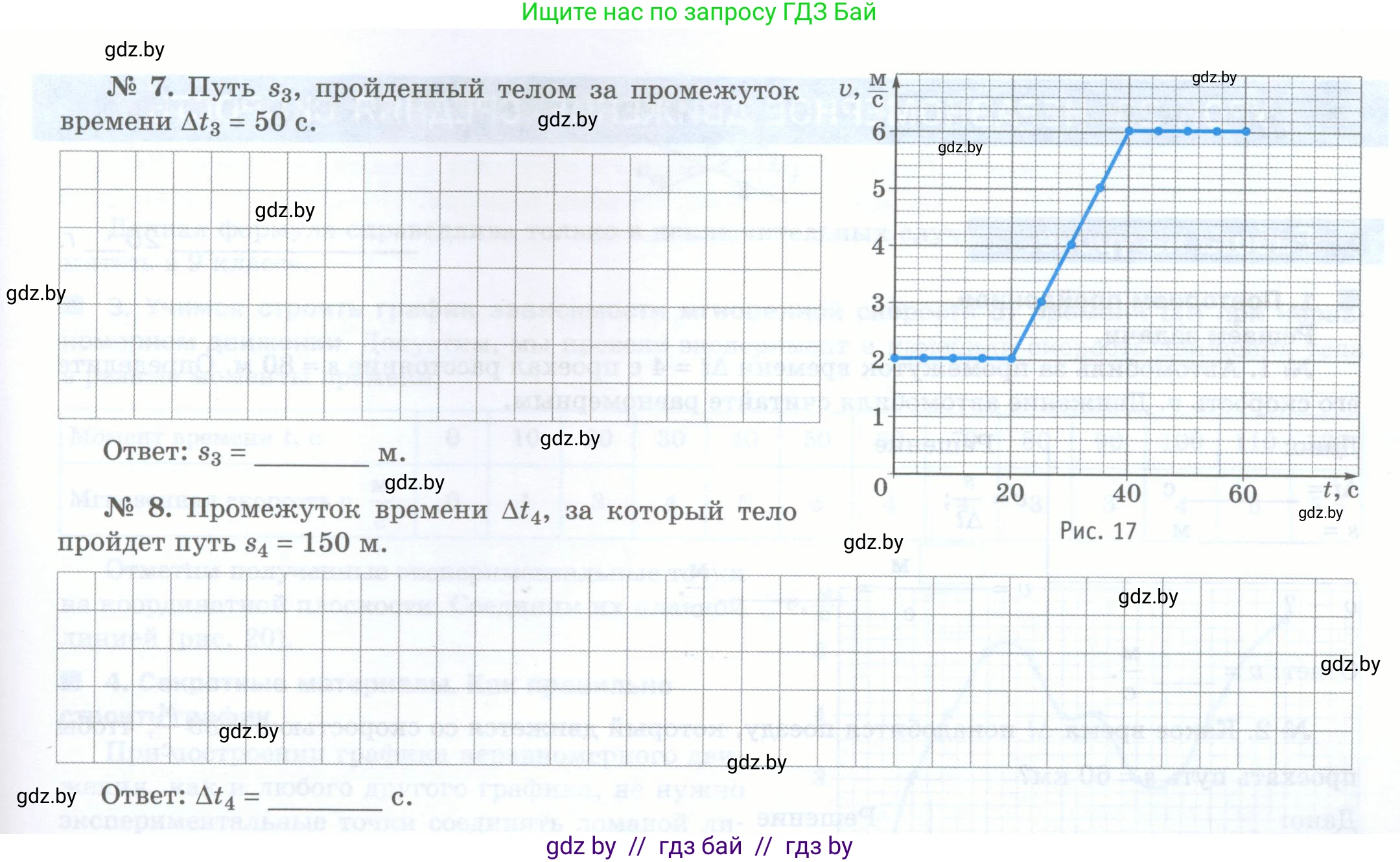
Используя график зависимости скорости движения от времени $v(t)$ (рис. 17), определите:

№ 5. Скорость движения тела $v_1$ в момент времени $t_1 = 30$ с.

Ответ: $v_1 = \text{\_\_\_\_\_\_ } \frac{\text{м}}{\text{с}}$.

№ 6. Путь $s_2$, пройденный телом за промежуток времени $\Delta t_2 = 20$ с.

Ответ: $s_2 = \text{\_\_\_\_ } м.$

№ 7. Путь $s_3$, пройденный телом за промежуток времени $\Delta t_3 = 50$ с.

Ответ: $s_3 =\text{\_\_\_\_ } м.$

№ 8. Промежуток времени $\Delta t_4$, за который тело пройдет путь $s_4 = 150$ м.

Ответ: $\Delta t_4 =\text{\_\_\_\_ }с.$

№ 1. Путь s₁, пройденный телом I за промежуток времени Δt₁ = 20 с.

Для определения пути, пройденного телом I за 20 с, находим на оси времени (ось абсцисс) значение $t = 20$ с. Проводим вертикальную линию до пересечения с графиком I. От точки пересечения проводим горизонтальную линию до оси пути (ось ординат). Получаем значение пути $s₁ = 100$ м.

Ответ: $s₁ = 100$ м.

№ 2. Скорости движения v₁ и v₂ обоих тел.

Дано:

График зависимости пути от времени s(t) для двух тел (рис. 16).

Найти:

$v₁, v₂$ - ?

Решение:

Графики зависимости пути от времени для обоих тел представляют собой прямые линии, проходящие через начало координат. Это означает, что тела движутся равномерно и прямолинейно. Скорость равномерного движения определяется по формуле $v = s/t$.
Для тела I выберем точку на графике, например, $t₁ = 20$ с. Из графика видно, что за это время тело прошло путь $s₁ = 100$ м. Тогда его скорость:
$v₁ = s₁ / t₁ = 100 \text{ м} / 20 \text{ с} = 5 \text{ м/с}$.
Для тела II выберем удобную точку на графике, например, $t₂ = 40$ с. За это время тело прошло путь $s₂ = 150$ м. Тогда его скорость:
$v₂ = s₂ / t₂ = 150 \text{ м} / 40 \text{ с} = 3.75 \text{ м/с}$.

Ответ: $v₁ = 5$ м/с, $v₂ = 3.75$ м/с.

№ 3. Расстояние между телами s₂ через Δt₂ = 40 с после начала движения.

Дано:

$Δt₂ = 40$ с

Найти:

$s₂$ - ?

Решение:

Расстояние между телами можно найти как разность путей, пройденных каждым телом за одно и то же время. Найдем пути, пройденные телами за $Δt₂ = 40$ с, используя данные графика или ранее вычисленные скорости.
Путь, пройденный телом I: $s_{I} = v₁ \cdot Δt₂ = 5 \text{ м/с} \cdot 40 \text{ с} = 200 \text{ м}$.
Путь, пройденный телом II: $s_{II} = v₂ \cdot Δt₂ = 3.75 \text{ м/с} \cdot 40 \text{ с} = 150 \text{ м}$.
Расстояние между телами $s₂$ равно разности этих путей:
$s₂ = s_{I} - s_{II} = 200 \text{ м} - 150 \text{ м} = 50 \text{ м}$.

Ответ: $s₂ = 50$ м.

№ 4. Промежуток времени Δt₃, через который расстояние между телами станет равным s₃ = 160 м.

Дано:

$s₃ = 160$ м
$v₁ = 5$ м/с
$v₂ = 3.75$ м/с

Найти:

$Δt₃$ - ?

Решение:

Расстояние между телами со временем увеличивается и в любой момент времени $\text{t}$ равно $s(t) = s_I(t) - s_{II}(t) = v₁t - v₂t = (v₁ - v₂)t$.
Скорость удаления тел друг от друга (относительная скорость) равна $v_{отн} = v₁ - v₂ = 5 \text{ м/с} - 3.75 \text{ м/с} = 1.25 \text{ м/с}$.
Время $Δt₃$, через которое расстояние между телами станет равным $s₃$, можно найти по формуле: $Δt₃ = s₃ / v_{отн}$.
$Δt₃ = 160 \text{ м} / 1.25 \text{ м/с} = 128 \text{ с}$.

Ответ: $Δt₃ = 128$ с.

№ 5. Скорость движения тела v₁ в момент времени t₁ = 30 с.

Для определения скорости тела в момент времени $t₁ = 30$ с, находим на оси времени (ось абсцисс) значение $t = 30$ с. Проводим вертикальную линию до пересечения с графиком $v(t)$. От точки пересечения проводим горизонтальную линию до оси скорости (ось ординат). Момент времени $t = 30$ с находится на участке равноускоренного движения (между 20 с и 40 с). В этой точке график проходит через отметку $v = 4$ м/с. Также, поскольку $t = 30$ с является серединой интервала, скорость будет равна среднему арифметическому скоростей в начале и конце интервала: $v₁ = (v(20) + v(40)) / 2 = (2 \text{ м/с} + 6 \text{ м/с}) / 2 = 4 \text{ м/с}$.

Ответ: $v₁ = 4$ м/с.

№ 6. Путь s₂, пройденный телом за промежуток времени Δt₂ = 20 с.

Дано:

$Δt₂ = 20$ с (от $t=0$ до $t=20$ с)
График зависимости скорости от времени v(t) (рис. 17).

Найти:

$s₂$ - ?

Решение:

Путь, пройденный телом, численно равен площади фигуры под графиком скорости. В промежутке времени от 0 до 20 с тело двигалось с постоянной скоростью $v = 2$ м/с.
Следовательно, пройденный путь $s₂$ равен площади прямоугольника с основанием $Δt₂ = 20$ с и высотой $v = 2$ м/с.
$s₂ = v \cdot Δt₂ = 2 \text{ м/с} \cdot 20 \text{ с} = 40 \text{ м}$.

Ответ: $s₂ = 40$ м.

№ 7. Путь s₃, пройденный телом за промежуток времени Δt₃ = 50 с.

Дано:

$Δt₃ = 50$ с (от $t=0$ до $t=50$ с)
График зависимости скорости от времени v(t) (рис. 17).

Найти:

$s₃$ - ?

Решение:

Путь, пройденный телом за 50 с, равен площади фигуры под графиком $v(t)$ от $t=0$ до $t=50$ с. Разобьем движение на три участка:
1. Участок от 0 до 20 с: равномерное движение. Путь $s_{0-20} = 2 \text{ м/с} \cdot 20 \text{ с} = 40 \text{ м}$.
2. Участок от 20 до 40 с: равноускоренное движение. Путь равен площади трапеции с основаниями 2 м/с и 6 м/с и высотой $(40 - 20) = 20$ с. $s_{20-40} = ((2+6)/2) \cdot 20 = 4 \cdot 20 = 80 \text{ м}$.
3. Участок от 40 до 50 с: равномерное движение. Путь $s_{40-50} = 6 \text{ м/с} \cdot (50 - 40) \text{ с} = 6 \cdot 10 = 60 \text{ м}$.
Общий путь $s₃$ равен сумме путей на этих участках:
$s₃ = s_{0-20} + s_{20-40} + s_{40-50} = 40 \text{ м} + 80 \text{ м} + 60 \text{ м} = 180 \text{ м}$.

Ответ: $s₃ = 180$ м.

№ 8. Промежуток времени Δt₄, за который тело пройдет путь s₄ = 150 м.

Дано:

$s₄ = 150$ м
График зависимости скорости от времени v(t) (рис. 17).

Найти:

$Δt₄$ - ?

Решение:

Найдем, на каком участке движения тело пройдет путь 150 м.
1. За первые 20 с тело прошло путь $s_{0-20} = 40 \text{ м}$. Это меньше 150 м.
2. За время с 20 по 40 с тело прошло путь $s_{20-40} = 80 \text{ м}$.
Суммарный путь за 40 с: $s_{0-40} = s_{0-20} + s_{20-40} = 40 \text{ м} + 80 \text{ м} = 120 \text{ м}$. Это также меньше 150 м.
3. Оставшийся путь, который тело должно пройти: $s_{ост} = s₄ - s_{0-40} = 150 \text{ м} - 120 \text{ м} = 30 \text{ м}$.
Этот путь тело проходит на третьем участке (после 40 с), двигаясь с постоянной скоростью $v = 6$ м/с. Время, необходимое для этого: $Δt_{ост} = s_{ост} / v = 30 \text{ м} / 6 \text{ м/с} = 5 \text{ с}$.
Общее время движения $Δt₄$ равно времени первых двух участков плюс время на третьем участке: $Δt₄ = 40 \text{ с} + Δt_{ост} = 40 \text{ с} + 5 \text{ с} = 45 \text{ с}$.

Ответ: $Δt₄ = 45$ с.